|
|
|
|
The Best Weapon |
最強兵器 決定戦
第53回(空軍1) 固定翼機と 反重力型輸送機器 |
|
MEGA TRAVELLER
|
|
|
|
エアラフトは急に曲がれない |
|
|
|
|
|
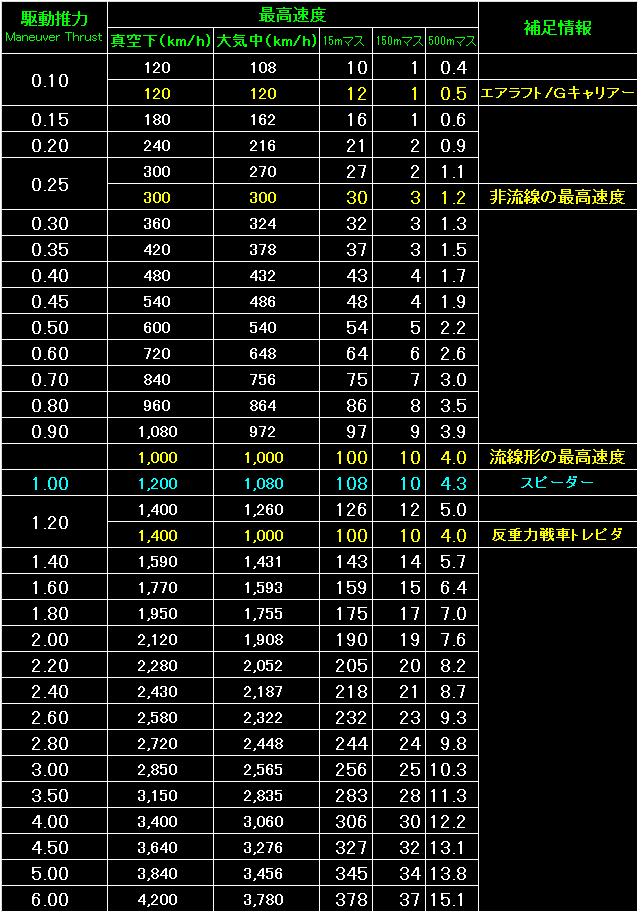
表の左端が駆動推力。 |

|
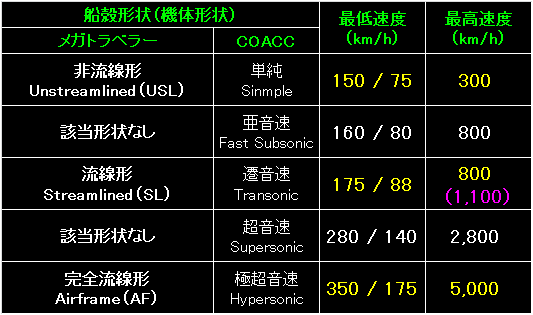
表の左側が船殻形状(機体形状)。 |

|
表の左側が大気タイプ(UWPコード)です。 |
|
機体形状と最低速度の表を「ハード・タイムズ、p.85」から抜粋しました。 |
|
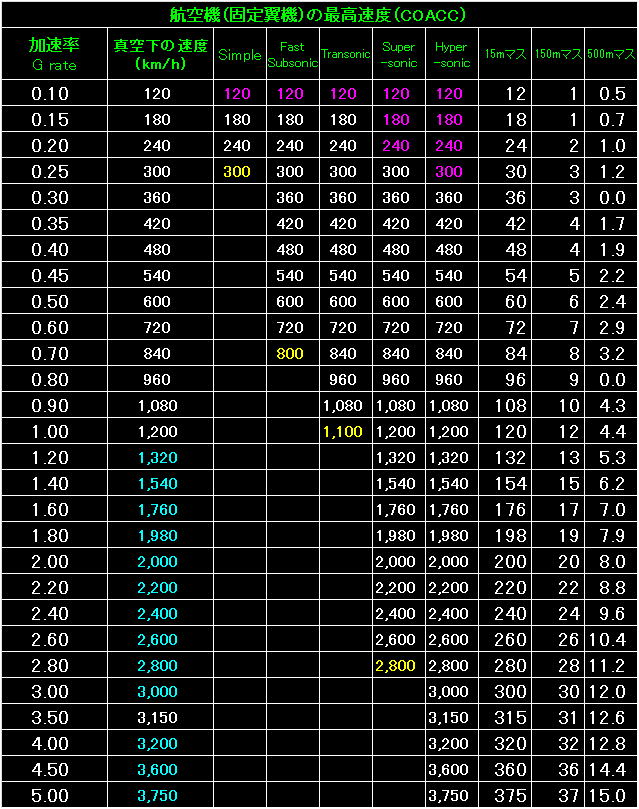
表の左端が加速率。 |
|
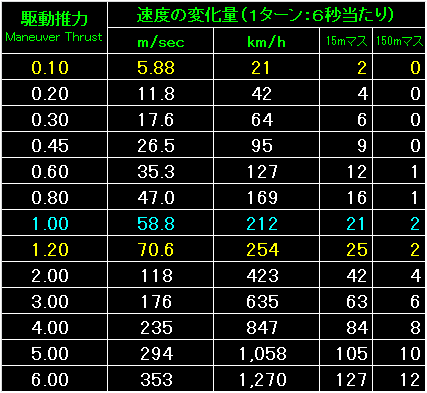
表の左端が駆動推力。 |
|
|
|
|
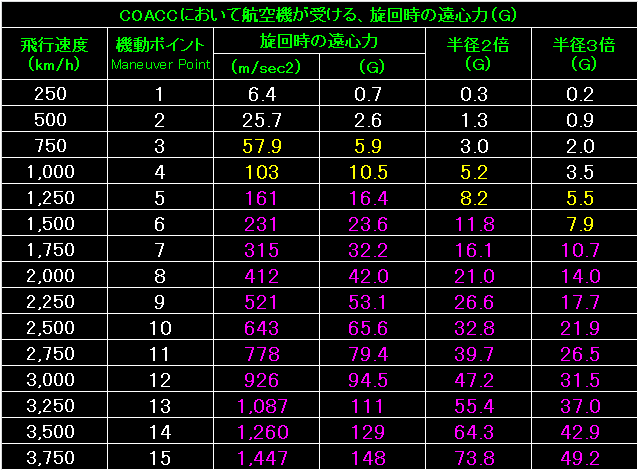
|
表の左端が航空機の飛行速度。 |
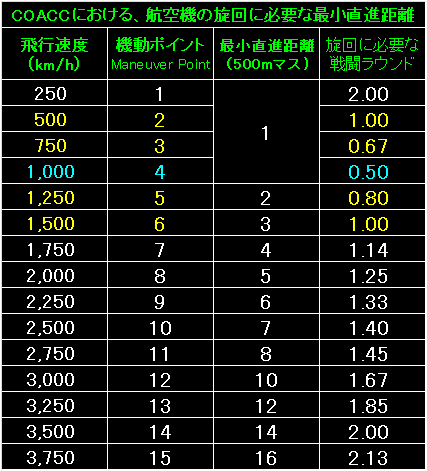
|
表の左端は今回も航空機の飛行速度と機動ポイントです。 |
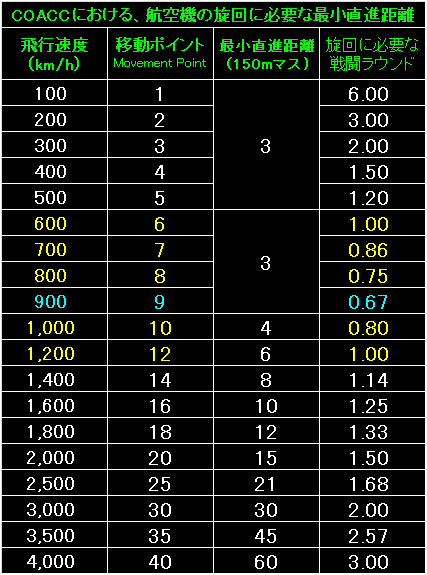
|
1マスのスケールを500mマスから150mマスに変更(30%の縮小)。 |
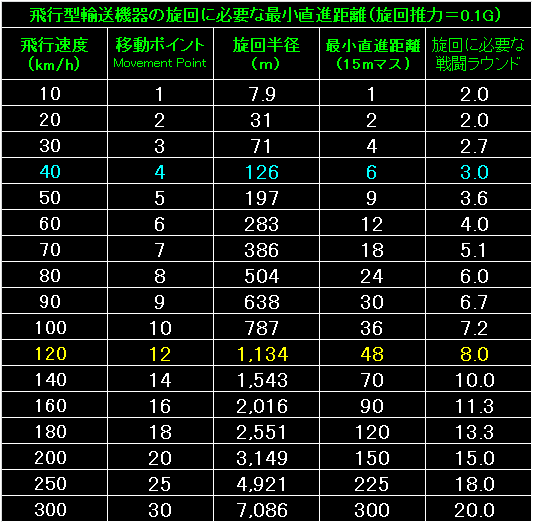
|
表の左端は飛行型輸送機器の飛行速度と移動ポイントです。 |
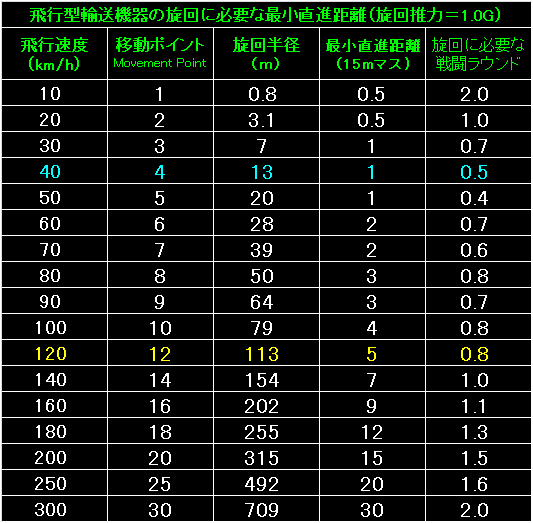
|
表の左端は飛行型輸送機器の飛行速度と移動ポイントです。 |
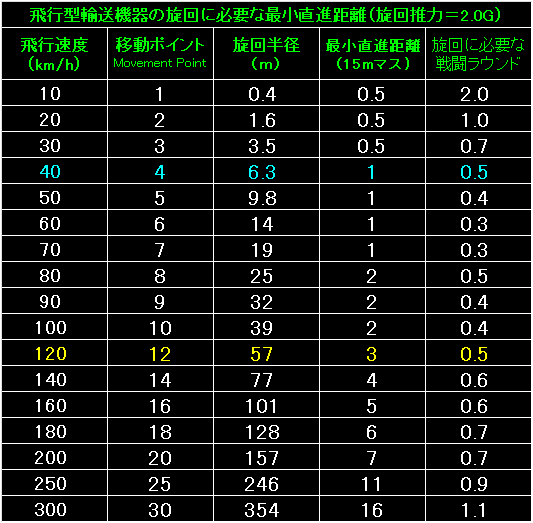
|
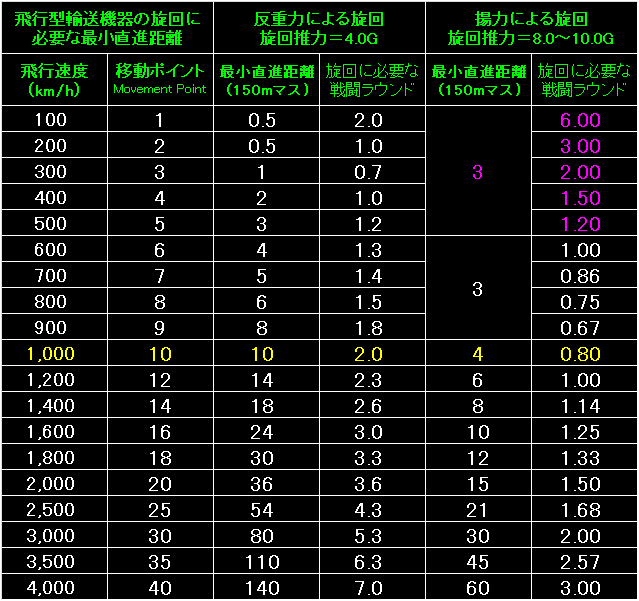
旋回推力が0.1Gから1.0Gまで増えた場合に比べてしまうと
それほど劇的な変わり方ではありませんが、旋回半径はほぼ半分に、最小直進距離も半分前後まで減りました。 |
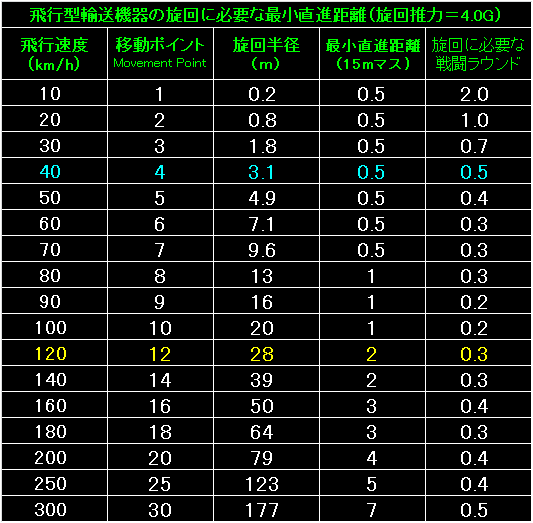
|
実に素晴らしい旋回能力ですが、200%の場合も400%の場合も、
オーバードライブには何らかのペナルティを設けておくべきでしょう。 |
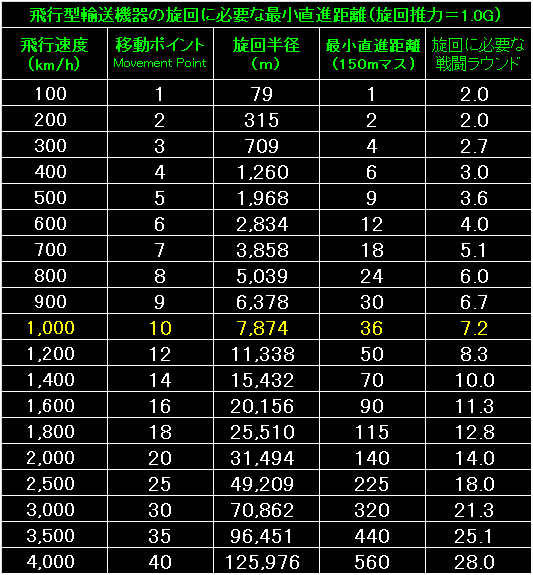
|
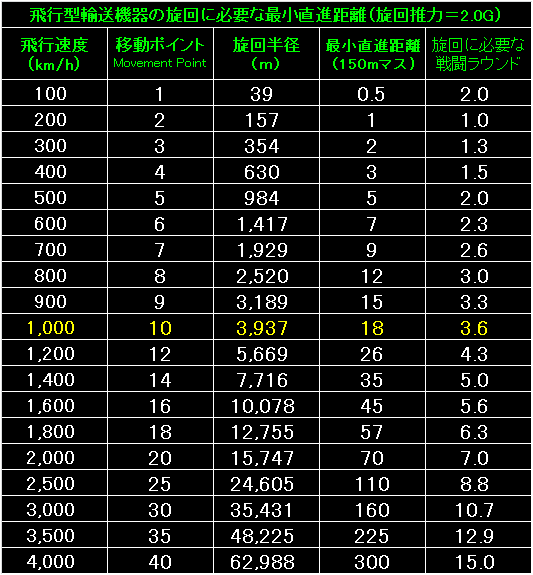
表の左端は飛行型輸送機器の飛行速度と移動ポイントです。 |
|
旋回推力が2倍に増えた御蔭で、旋回半径はほぼ半分に、最小直進距離も半分に減りました。 |
|
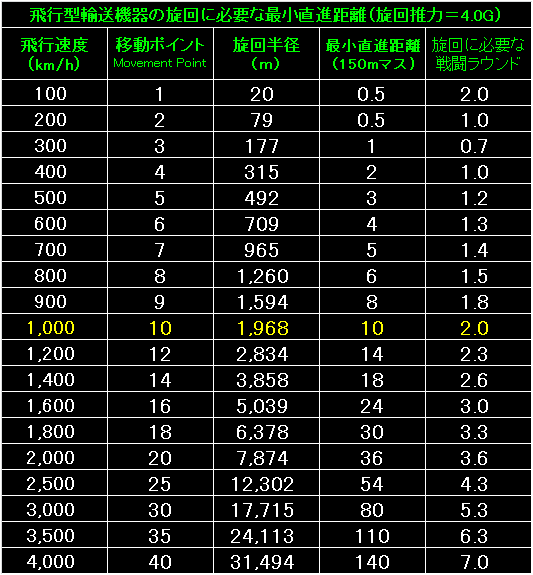
旋回推力を4.0Gまで増やしても、1,000km/hで飛行するスピーダーと反重力戦車トレピダは、
最小直進距離が10マスまでしか減りませんでした。 |
|
今回も、表の左端は飛行型輸送機器の飛行速度と移動ポイントです。 |
|
|
|
|
|
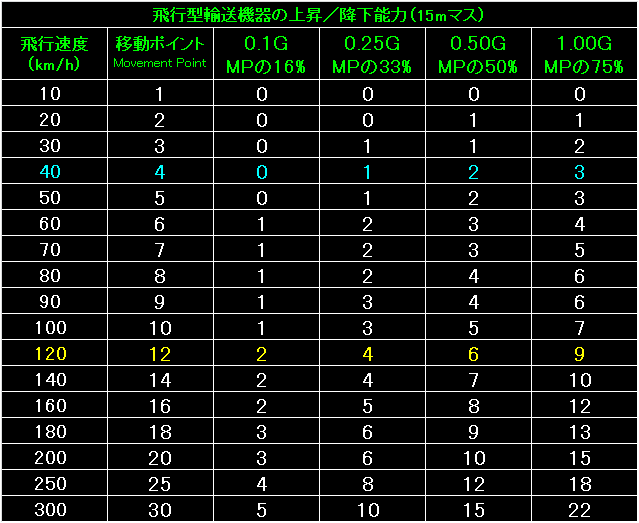
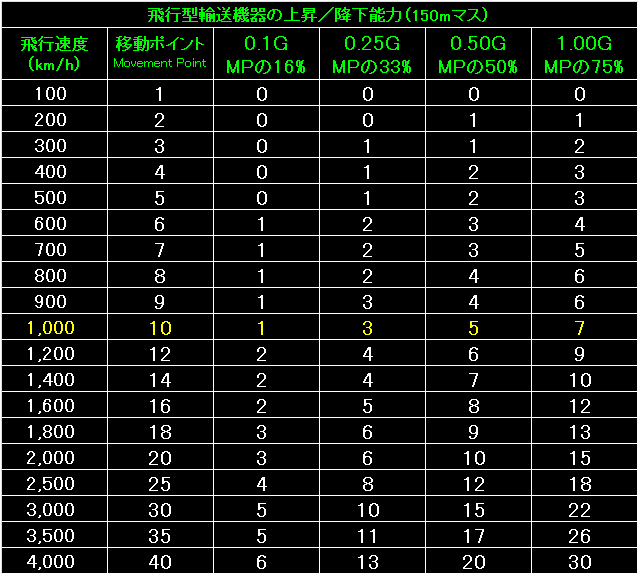
表の左端は飛行型輸送機器の飛行速度と移動ポイントです。 |
|
今回も、表の左端は飛行型輸送機器の飛行速度と移動ポイント。 |
|
|
|
|
|
|
|
|