|
|
|
|
The Best Weapon |
最強兵器 決定戦
第54回(空軍2) 回転翼機と 飛行船 |
|
MEGA TRAVELLER
|
|
|
|
NOE飛行の大きな利点は |
|
|
|
|
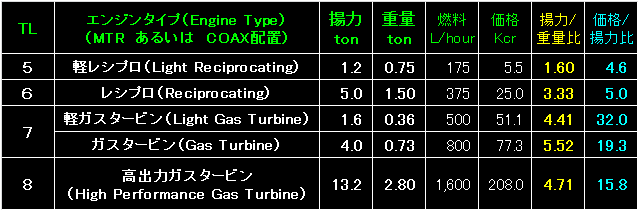
|
MTR/COAX配置というのは、回転翼の配置方式です。 |
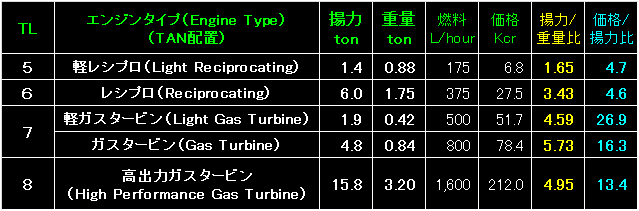
|
TAN配置とはタンデム・ローター配置:Tandem Main Rotors のことであり、
機体の前後に同じ大きさの主ローターを1枚ずつ配置した方式です。 |

|
実はLGTA配置には正式な名称がありません。
英文では Light Gearbox and Transmission Assemblies と書かれていますので、
強引に和訳すれば軽量回転翼となるでしょう。 |
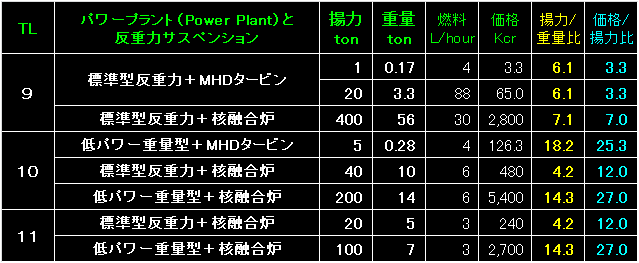
|
表の作り方はこれまでと同じですが、回転翼の代わりに反重力式サスペンション、
エンジンの代わりにパワープラント、具体的には核融合炉とMHDタービンを搭載した場合の
揚力、重量、
燃料消費量(L/Hour)、価格(Kcr)、
揚力/重量比、価格/揚力比を並べました。 |
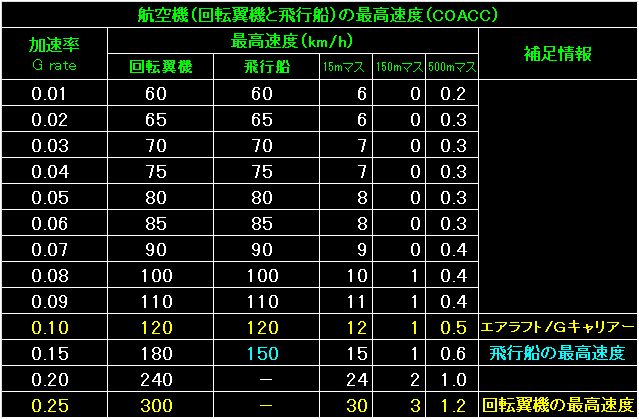
|
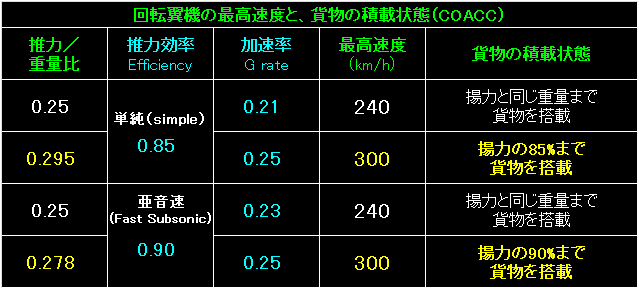
表の左端が加速率。 |
|
機体形状として「亜音速(Fast subsonic)」を選択することで、最高速度300km/hを出す際、
貨物(武装や燃料)を5%も余計に積めるのだと考えれば、機体形状の選択にも納得できます。 |
|
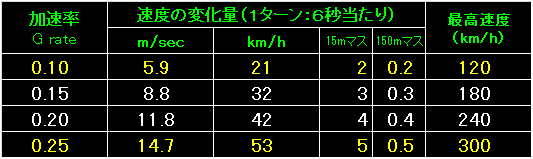
表の左端が加速率。 |
|
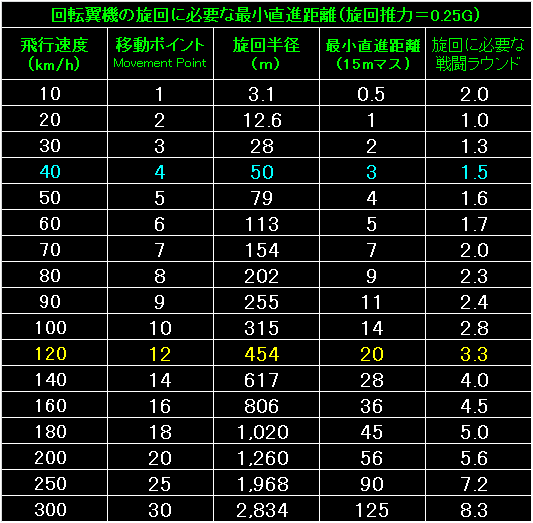
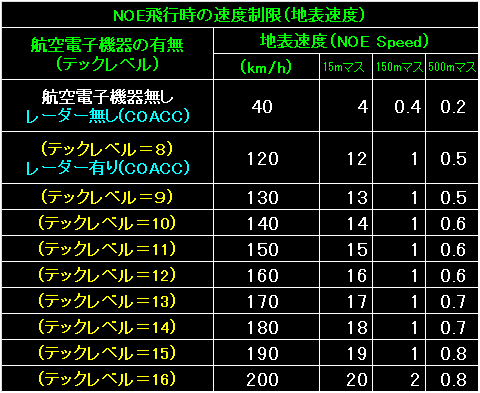
表の左端は回転翼機の飛行速度と移動ポイントです。 |
|
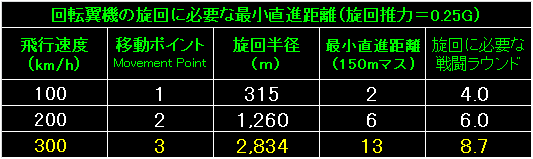
この表のスケールは150mマスです。 |
|
|
|
|
|
表の左端が航空電子機器の有無と、
装備している場合は航空電子機器のテックレベルを表しています。 |
|
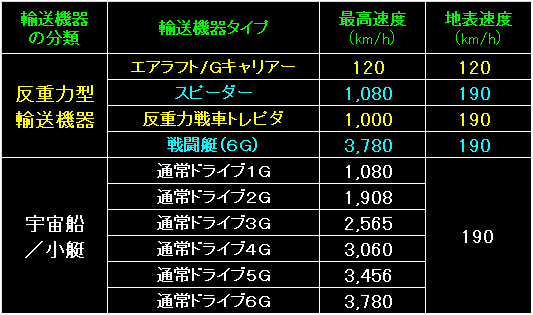
表の左端が、輸送機器の分類。 |

|
表の左端が固定翼機の飛行速度。 |
|
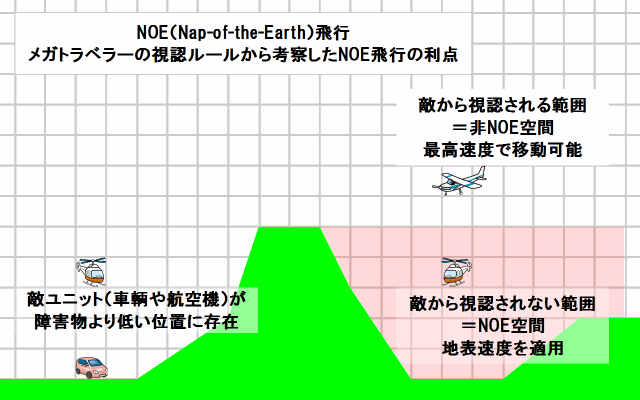
図13 メガトラの視認ルールから考察したNOE飛行の利点 |
|
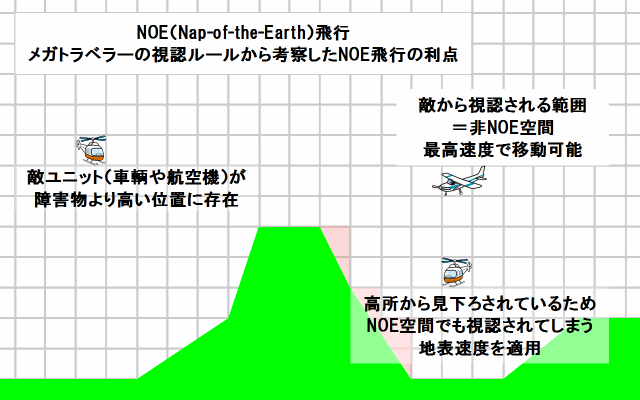
図14 メガトラの視認ルールから考察したNOE飛行の利点 |
|
|
|
|
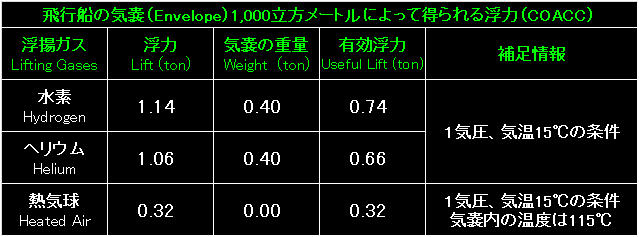
|
表の左端が、気嚢の中へ充填する浮揚ガス(Lifting Gases)の種類。 |
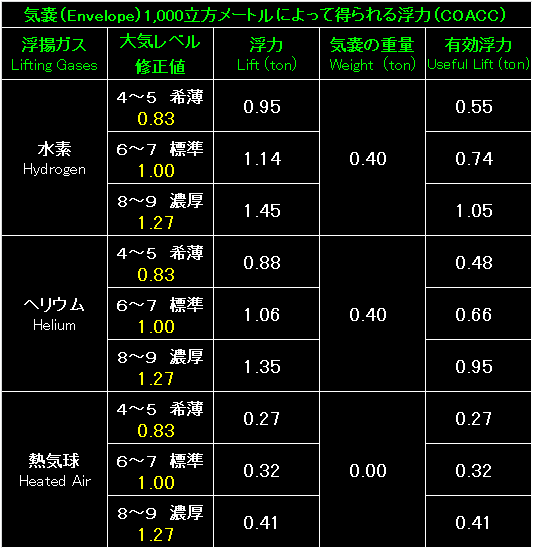
|
表の左端は今回も浮揚ガス(Lifting Gases)の種類。 |
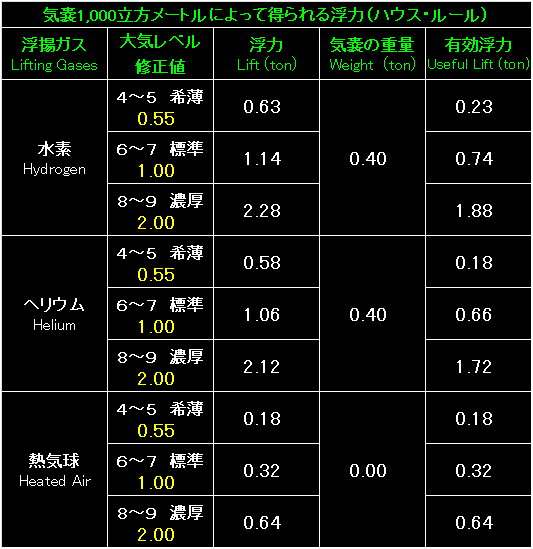
|
有効浮力が大きく変化しました。 |

|
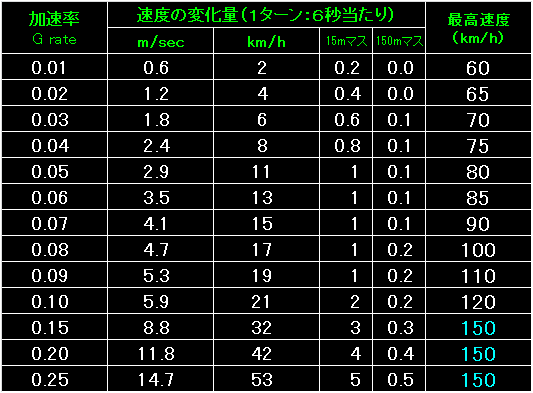
表の左端が加速率。 |
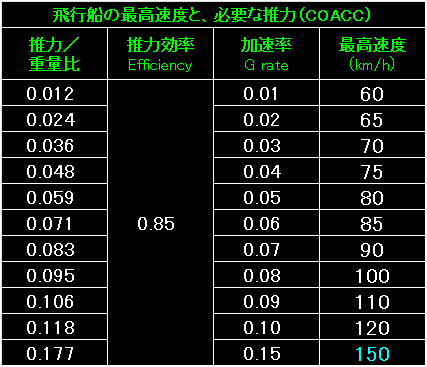
|
表の左端が推力/重量比。 |
|
表の左端が加速率。 |
|
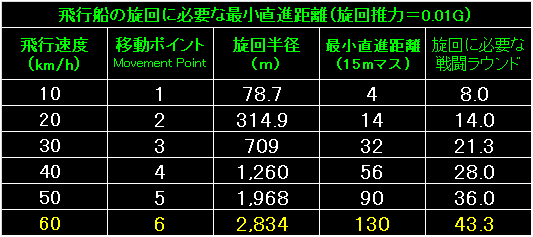
表の左端は飛行船の飛行速度と移動ポイントです。 |
|
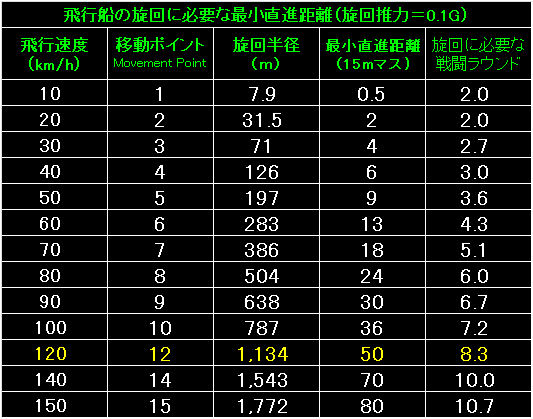
今回も表の左端は飛行船の飛行速度と移動ポイント。 |
|
|
|
|