|
|
|
|
The Best Weapon |
最強兵器 決定戦
第55回(空軍3) 羽ばたき機と ホバークラフト |
|
MEGA TRAVELLER
|
|
|
|
ホバークラフトは斜面を走れない |
|
|
|
|
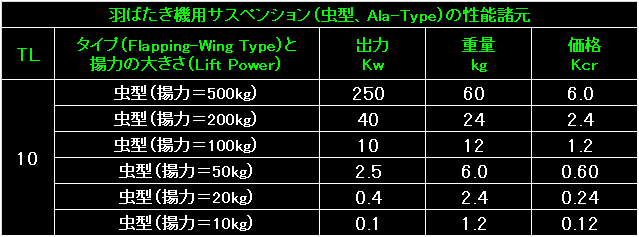
|
表の左端は、このタイプの羽ばたき翼を初めて利用できるようになるテックレベルです。 |
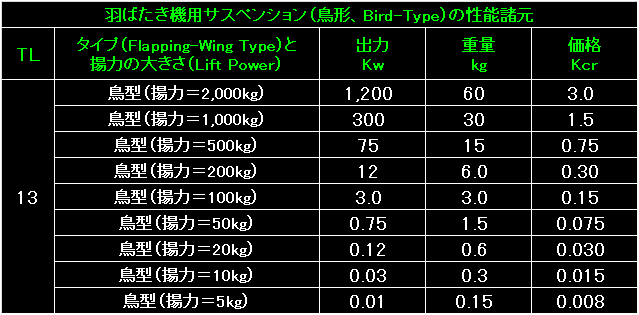
|
今回も表の左端は、このタイプの羽ばたき翼を初めて利用できるようになるテックレベル。 |
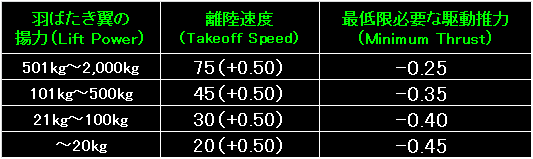
|
表の左端は羽ばたき翼が発生する揚力の大きさ。 |
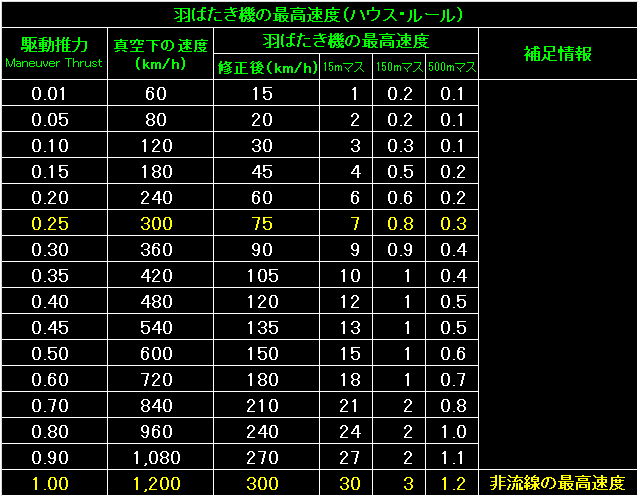
|
表の左端は駆動推力。 |
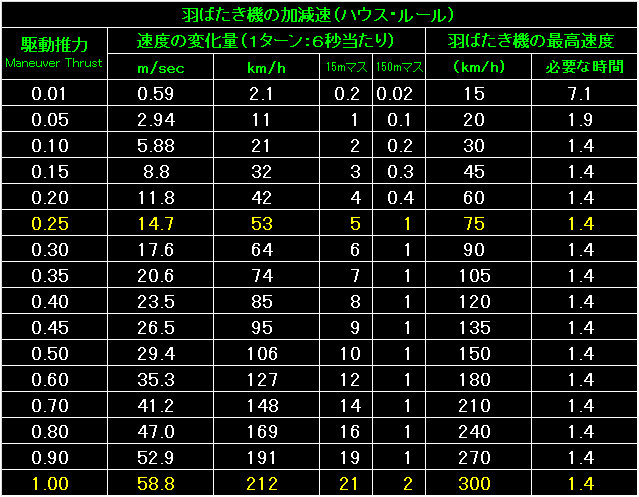
|
表の左端が駆動推力。 |
|
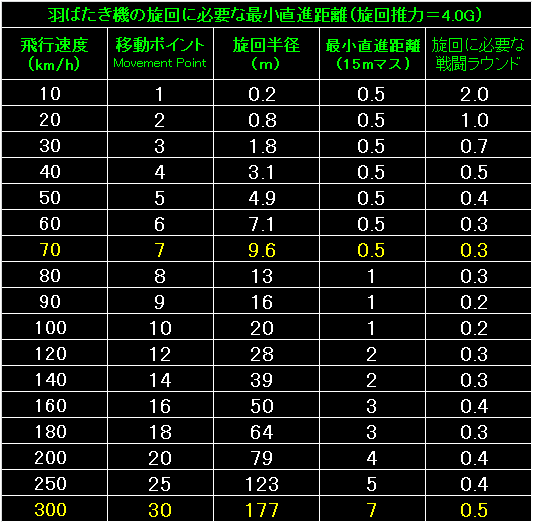
表の左端は羽ばたき機の飛行速度と移動ポイント。 |
|
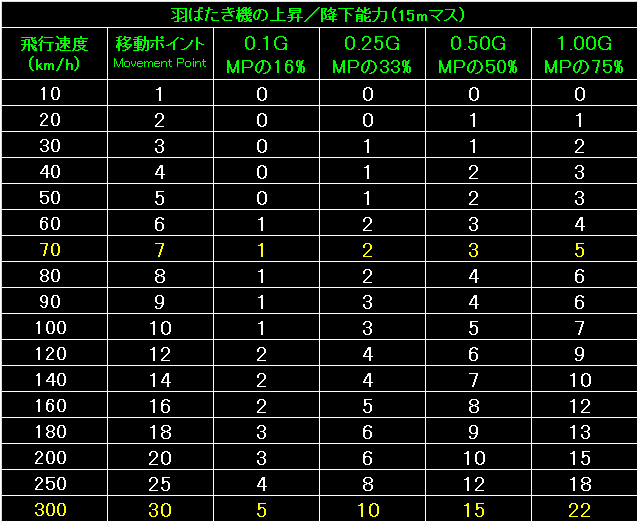
表の左端は羽ばたき機の飛行速度と移動ポイントです。 |
|
|
|
|
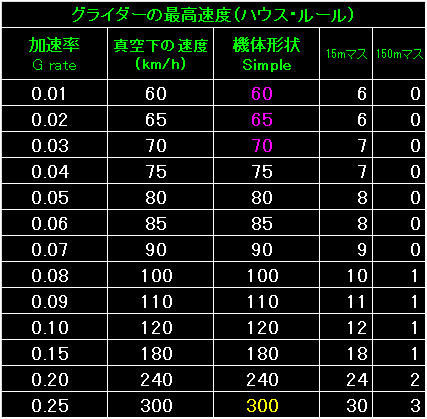
|
表の左端が加速率。 |
|
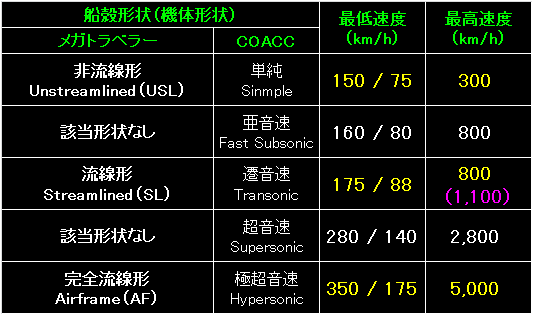
機体形状と最低速度の表を「ハード・タイムズ、p.85」から抜粋しました。 |
|
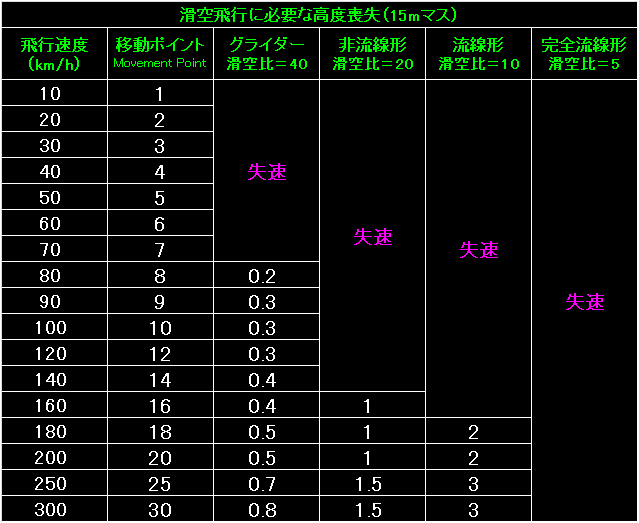
表の左端は滑空する航空機の飛行速度と移動ポイント。 |
|
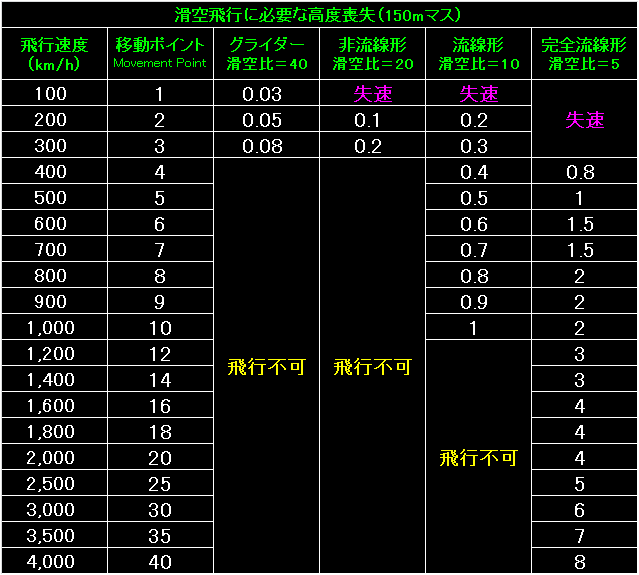
表の左端は今回も滑空する航空機の飛行速度と移動ポイント。 |
|
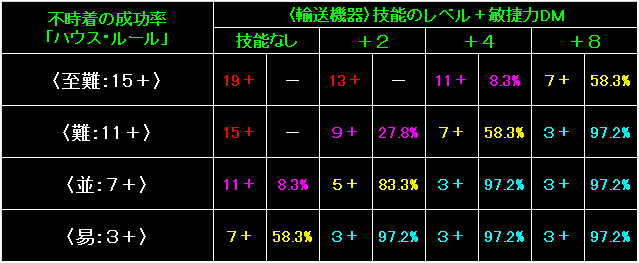
表の左端は不時着の行為判定の難易度です。 |
|
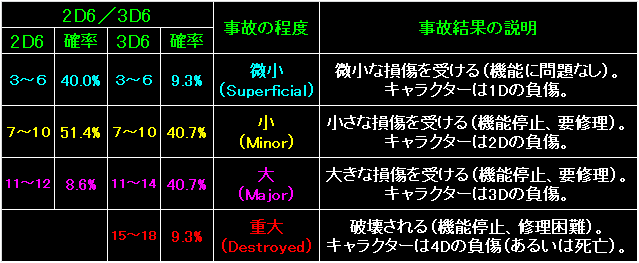
表の左は、サイコロの目と、特定の目が出る確率です。 |
|
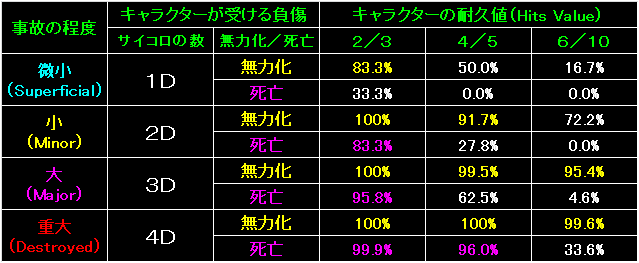
表の左端が事故の程度。 |
|
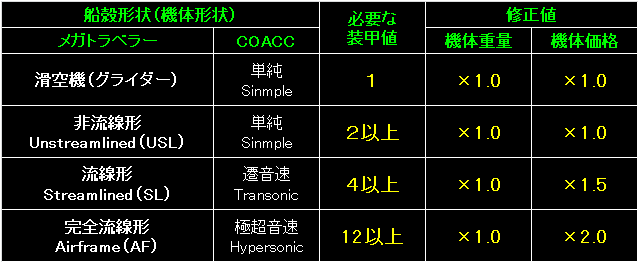
表の左端は、メガトラの輸送機器設計ルールで示されている3つの船殻形状と、今回新たに追加した滑空機(グライダー)形状。 |
|
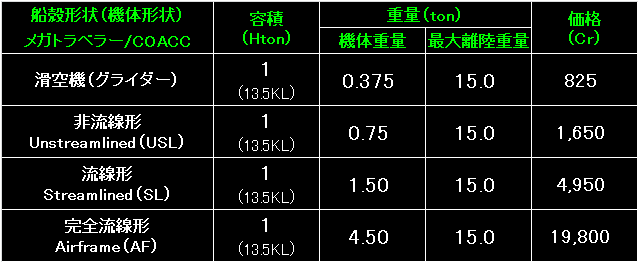
表の左端は、4種類の機体形状。 |
|
|
|
|
|
表の左端が駆動推力。 |
|
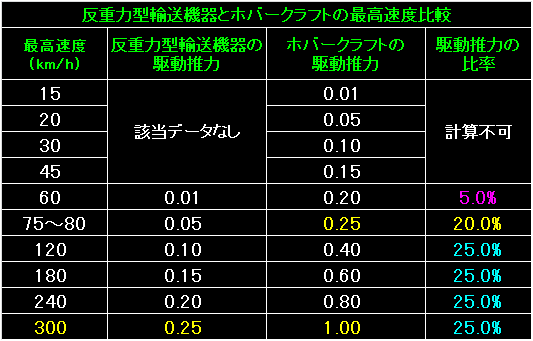
今回、表の左端は最高速度です。 |

|
表の左側にテックレベル。 |
|
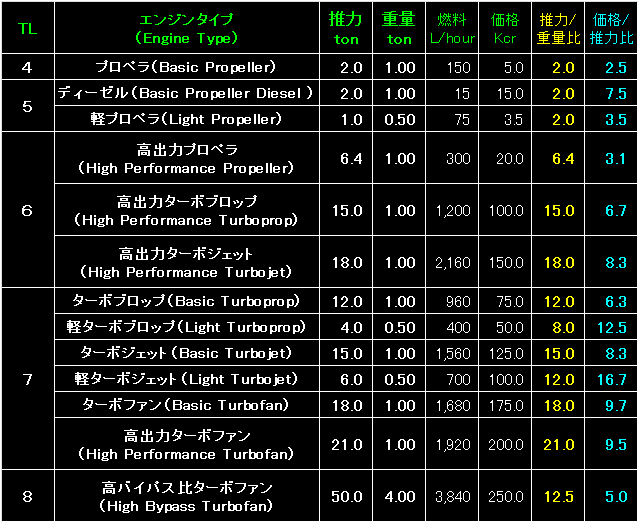
例によって、表の左端はテックレベル。 |
|
表左端のテックレベルとエンジン・タイプ(Engine Type)については、
これまでと同様。 |
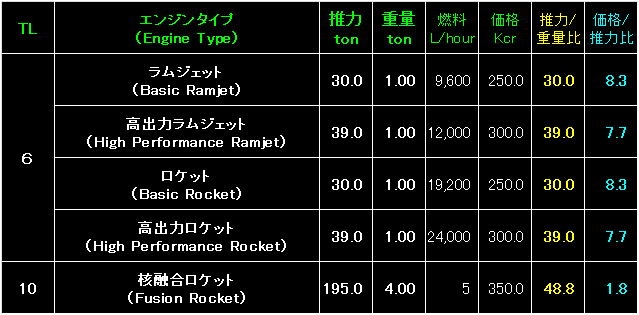
|
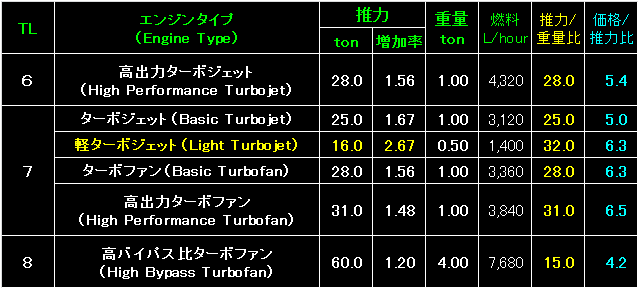
左端のテックレベルとエンジン・タイプ(Engine Type)は同様。 |
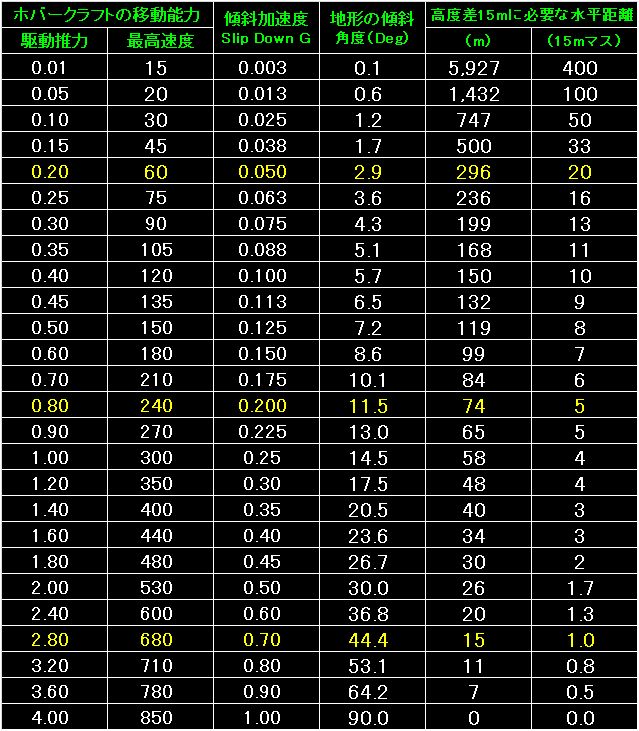
|
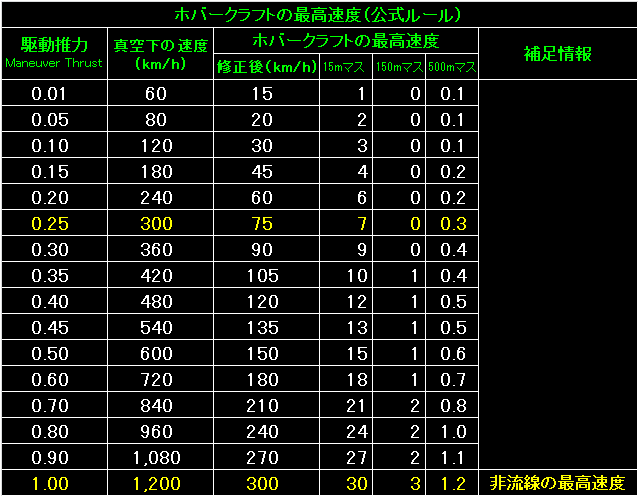
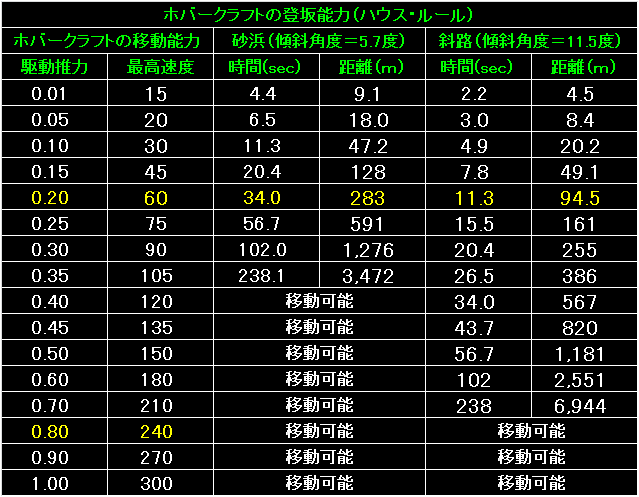
表の左端はホバークラフトの移動能力で、輸送機器設計ルールを使って求めた
駆動推力と最高速度を並べてあります。 |
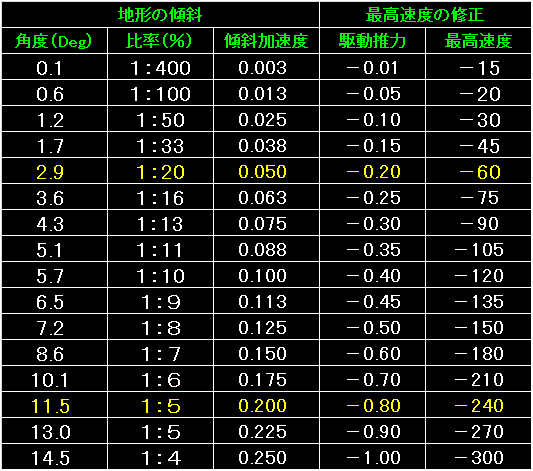
|
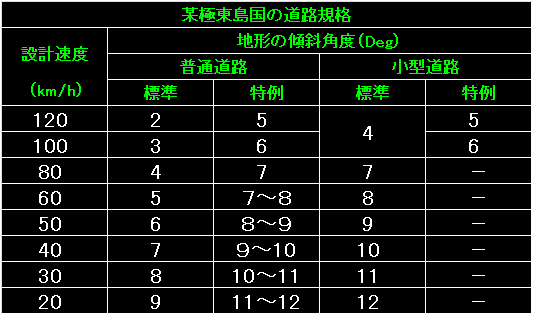
表の左は、地形の傾斜。 |
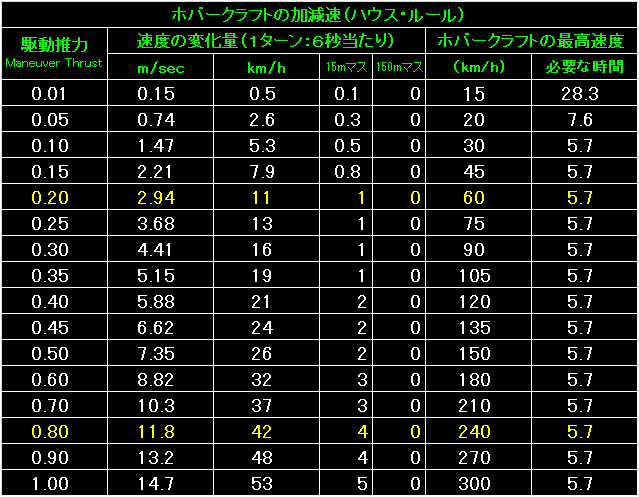
|
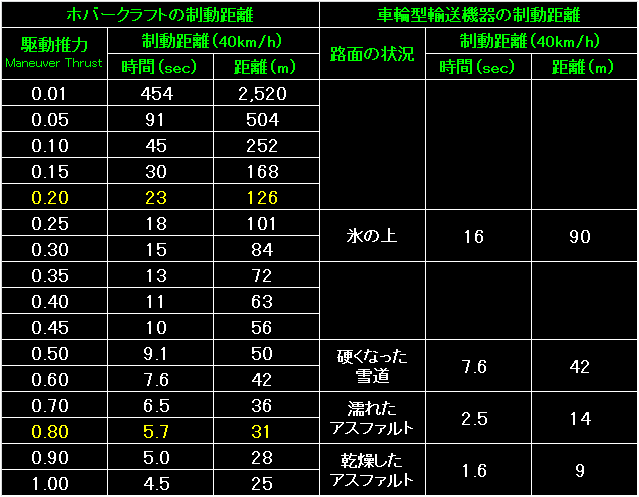
表の左端が駆動推力。 |
|
表の左側は、ホバークラフトの制動距離。 |
|
表の左端は今回もホバークラフトの移動能力です。 |
|
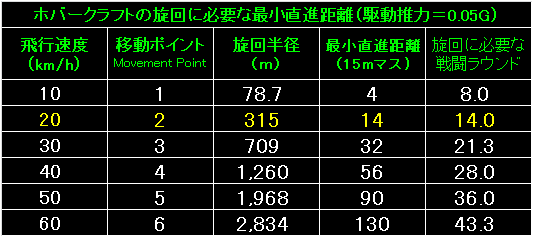
表の左端はホバークラフトの飛行速度(km/h)と移動ポイント。 |
|
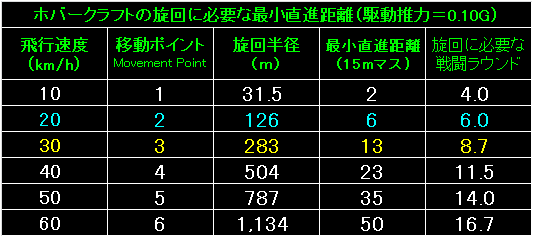
ホバークラフトが駆動推力=0.10Gで旋回した場合の
旋回半径(m)と最小直進距離です。 |
|
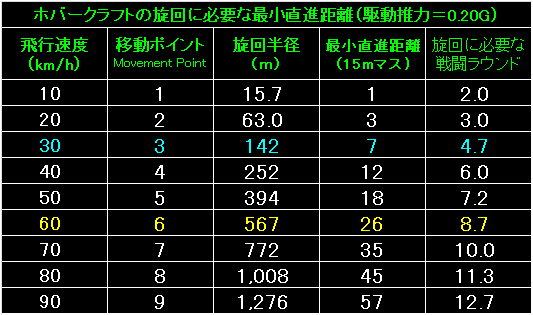
ホバークラフトが駆動推力=0.20Gで旋回した場合の
旋回半径と最小直進距離です。 |
|
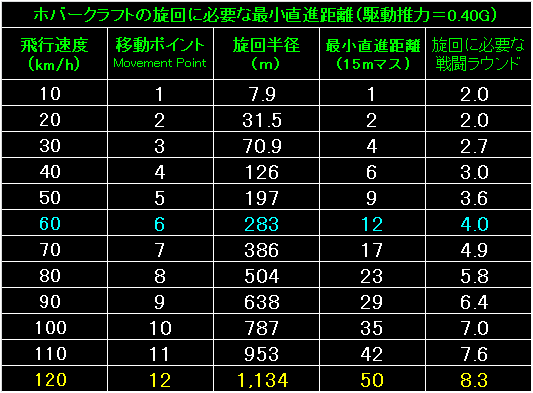
今度は、ホバークラフトが駆動推力=0.40Gで旋回した場合の
旋回半径と最小直進距離です。 |
|
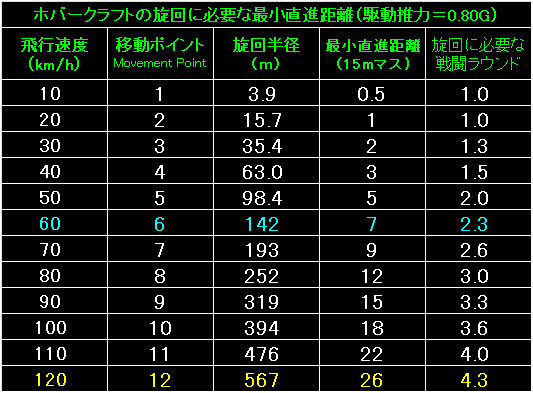
最後に、ホバークラフトが駆動推力=0.80Gで旋回した場合の
旋回半径と最小直進距離を計算しました。 |
|
上の表は道路の前後方向の傾斜角度です。 |
|
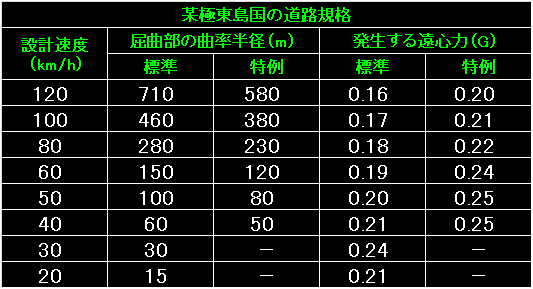
この表は、屈曲部(カーブ)の曲率半径を示しています。単位はメートル(m)。 |
|
|
|
|