「もしも月がなかったら（ニール・Ｆ・カミンズ著　竹内均監修　東京書籍）」の、読後レポート第三弾です。
　この本はタイトル通り、もしも月がなかったら、この地球はどんな環境になっていただろう、という思考実験を行ない、 その結果をまとめた書籍です。
　今回は５番目の仮想地球、グランスターを元ネタにして、考察してみましょう。



　もしも太陽の質量がもっと大きかったら？（仮想地球の５番目、グランスター）

　この本の中では、太陽の質量が1.5倍（スペクトル型はF2〜F3）であると想定して思考実験を行なっています。
　その場合、太陽の表面温度は6,700度。太陽の色は黄色ではなく、ほとんど白です。
　照射エネルギー量が５倍に増えるため、地球を灼熱地獄に変えたくなかったら、 公転軌道を2.8AUの距離（軌道番号５）まで遠ざけなければなりません。
　公転周期は5.3年に増えますので四季が５倍の長さに延び、夏の暑さ、冬の寒さはさらに厳しくなります。
　著者は、長い冬による「氷河作用の暴走（全球凍結）」を心配していました。

　暑さと寒さが厳しくなる件について、私は少なからぬ疑問を感じます。
　四季の長さが変わることはともかく、グランスター全体が受け取るエネルギー量自体は地球と変わりません。 大気と海水の循環が熱のアンバランスを修正してくれるのであれば、暑さと寒さの程度が変わることはなく、 ただ単にその暑さと寒さが長く続くだけなのではないでしょうか？
　冬が長く続きますから、植物にとっては日照不足が、動物には食糧不足が、深刻な問題となるかも知れませんが。



　また、主恒星のスペクトルが異なることで、太陽光の成分も異なってきます。
　例えば、グランスターの主恒星は表面温度が高いため、太陽光は紫外線成分をずっと多く含むようになるでしょう （著者は１千倍以上だと述べていますが、算定基準が分かりません）。
　強力な紫外線を防ぐため、グランスターの大気には濃厚なオゾンが含まれていることになります。 ひょっとしたら高濃度のオゾンが地表付近に存在しているかも知れません（オゾンは地球原産の生命にとって有毒です）。
　そうでなければグランスターの地表には直接、有害な紫外線が大量に降り注いでいるでしょう。 著者は、動物がすべて夜行性化するとか、紫外線を防ぐために厚い甲羅や毛皮を纏うようになるだろうと述べています。

　これもちょっと不思議な話ですね。
　そもそもオゾンが存在するためには酸素が必要であり、酸素が発生するために植物が必要なことも間違いありません。 少なくともグランスターの水中（海中）には立派な生態系が出来上がっているのではないでしょうか。

　また、生物はしたたかなものですから、有害なものがあればあったなりの進化を遂げるものです。 そして進化は、単に有害な紫外線を遮蔽するといったことに終始するばかりではありません。
　地球原産の動植物でさえ、進化の過程で猛毒の酸素を利用する術を身に付けました。 紫外線の影響で発生する有害な活性酸素を無効化、あるいは逆にエネルギー源として利用する等、 様々な進化の可能性が考えられます。

　まぁ、人類の生存に適した環境とは言えませんが、必ずしも現地の動物が夜行性化したり、甲羅や毛皮を発達させる必要はないでしょう。
　むしろ紫外線量が増え、太陽エネルギーの総量が増えることで物を食べなくても動き回れる 光合成動物が発生するかもしれません。 ちなみに彼らの肌の色は良くイメージされる植物人の「緑」ではなく、 チクラドリア人のような「レンガ色」でしょう。 スペクトル型が変われば、光合成に使われる色素の色も変わりますから。



　という訳で、私は著者のイメージするグランスターの風景（生態系）には納得できません。 トラベラーの世界観にも似合いませんね。
　そこで私は自分なりの解釈を加え、トラベラー宇宙の太陽光を想像してみることにしました。



　ソル星系の主恒星である太陽は、スペクトルＧ２型の主系列星（トラベラーの呼び方では規模�Xの恒星）です。 人類を始めとする地球原産の生物は、スペクトルＧ型の太陽光に適応して、進化してきました。
　しかし、Ｇ型のスペクトルを持つ恒星は、それほどありふれたものではありません。
　トラベラーの星系作成ルールで表現されている通り、多くの星系において、星系の主恒星はＭ型（55.6％）であり、 次にＦ型（16.7％）、３番目がＫ型（13.9％）、 そして４番目に多いタイプがＧ型（11.1％）、５番目がＡ型（2.8％）なのです。

　Ｇ型以外の恒星を主恒星に抱く星系において、太陽光はどのような姿になっているのでしょうか。
　太陽光を浴びる地上はどのような情景なのか、考察してみます。

　今回の考察については、異なる太陽光下の自然環境や生態を想像する上で、橘様から多くの助言を頂きました。
　感謝します。

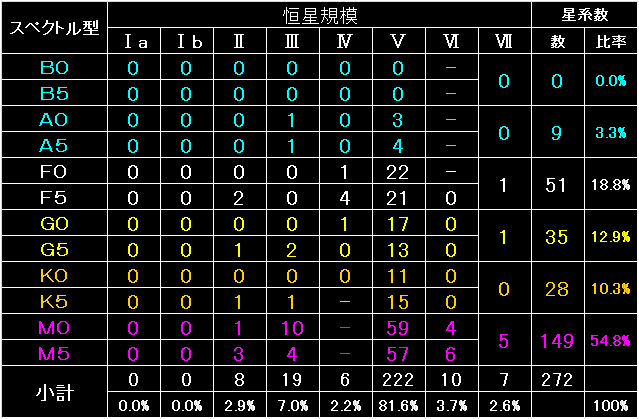
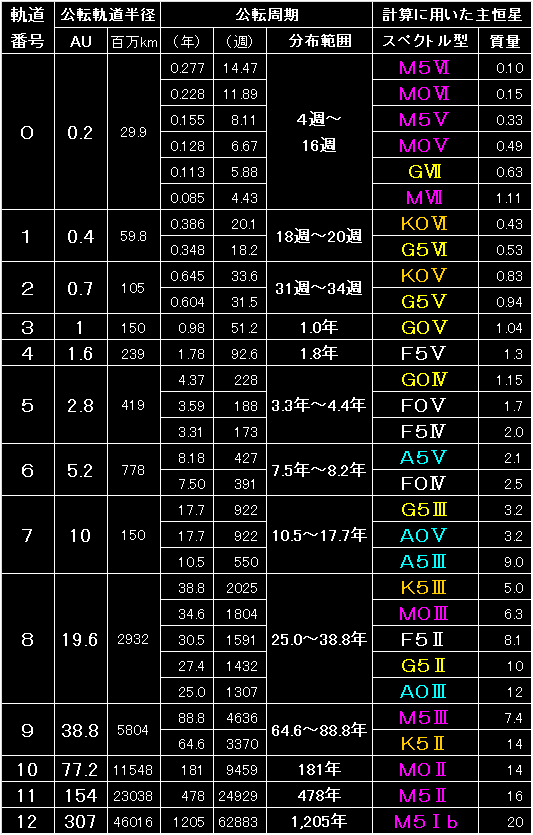
　という訳で例の如く、スピンワード・マーチ宙域の帝国領272星系について、 主恒星のスペクトル型と恒星規模を調べてみました。
　伴星のスペクトル型は、星系内の居住世界の環境にほとんど影響しませんから、無視しています（調べてもいません）。

　まずは、主恒星のリストアップから。


　　　　　　表１　スピンワード・マーチ宙域の帝国領272星系における
　　　　　　　　　　　　　　　主恒星のスペクトル型分布

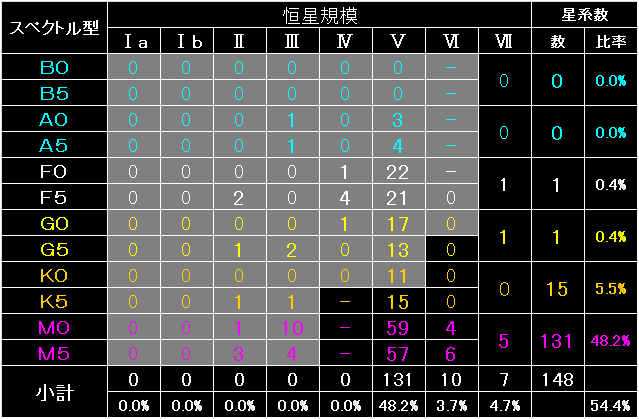
　272星系の内、恒星規模「�X（主系列星）」を主恒星としている星系は、 222星系（81.6%）でした。
　その次が恒星規模「�V（巨星）」の19星系（7.0％）で、 ３番目以降が規模「�Y（準矮星）」の10星系（3.7％）、 規模「�U（明るい巨星）」の８星系（2.9％）、 規模「�Z（白色矮星）」の７星系（2.6％）、 規模「�W（準巨星）」の６星系（2.2％）の順です。
　恒星規模「�X（主系列星）」が圧倒的多数であることは当然だとしても、 規模「�Z（白色矮星）」を主恒星とした星系が７つ（2.6％）も存在することに驚きを隠せません。
　何を好き好んで、白色矮星などに植民したのでしょうか。



　スペクトル型について注目すると最も多いスペクトルはＭ型で、その数は149星系。過半数を占めていました。
　ランダムに星系を選んだ場合、その星系の主恒星がＭ型である確率は54.8％です。
　お気付きだと思いますが、スペクトル型の分類に当たっては簡略化のため、 Ｍ０〜Ｍ４型をＭ０型、 Ｍ５〜Ｍ９型をＭ５型としました。 粗っぽい分類ですが、これだけ簡略化しなければスペクトル型の種類が多過ぎて計算できません。御容赦ください。

　次に多いスペクトル型は、Ｆ型です。星系数は51で、18.8%。

　３番目がようやく馴染み深い（太陽と同じ）スペクトルＧ型。 星系数は35で、12.9％を占めています。
　ランダムに選んだ星系の中で、Ｇ型の主恒星は８分の１しか存在しませんでした。

　４番目がスペクトルＫ型で、星系数は28、10.3％となっています。
　前項で述べた順位（３番目がＫ型で、４番目がＧ型）と入れ換わっていますが、 誤差の範囲内でしょう。

　最後がスペクトルＡ型。星系数は９つだけで、比率は3.3％。



　これらの主恒星について、その表面温度を調べてみました。
　これは「CT版偵察局、p.27」に掲載されていた資料を転載したものです。


　　　　　　　　　　　　　　表２　主恒星の表面温度

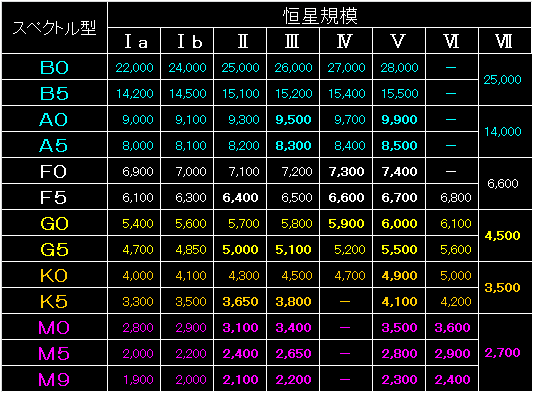
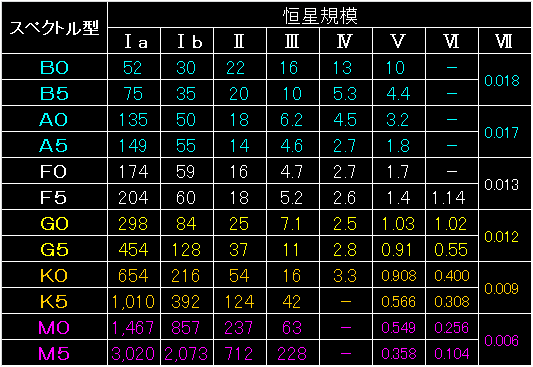
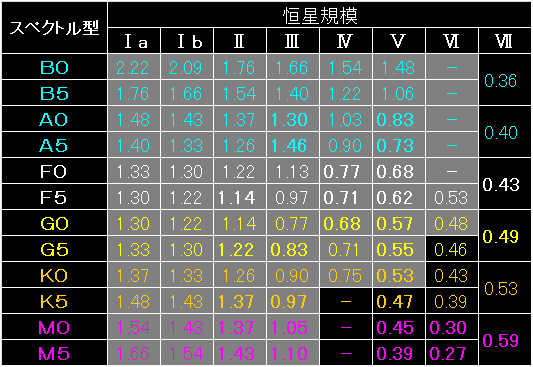
　スペクトル型と恒星規模に対応した恒星の表面温度を示しました。
　スピンワードマーチ宙域の帝国領内、272星系に存在する数値だけを太文字で強調しています。

　最も数の多いスペクトルＭ型は、 その表面温度が1,900〜3,600度の範囲に分布していました。
　実際に、帝国領内で見掛けられる表面温度はもう少し狭く、2,100〜3,600度の範囲ですが。

　次に多いスペクトルＦ型は、6,100〜7,400度の範囲。
　帝国領内で見られる温度は、6,400〜7,400度です。

　スペクトルＧ型は、4,500〜6,100度の範囲ですが、 帝国領内では4,500〜6,000度しか見られません。
　ちなみに、我らがソル（太陽）の表面温度は5,778度として扱われていました。 細分化されたスペクトル型ではＧ２型に該当する訳です。

　スペクトルＫ型は、3,300〜5,000度の範囲。
　帝国領内で見られる温度は、3,500〜4,900度です。

　スペクトルＡ型は、8,000〜14,000度の範囲。
　このスペクトル型は珍しいので帝国領内には９つしか存在せず、その温度範囲も8,300〜9,900度に限られました。

　スペクトルＢ型はさらに珍しく、帝国領内では見つかりません。 その温度範囲は14,200〜28,000度です。



　さて、これらの表面温度から、太陽光の成分比率を求めてみました。
　細かく分類しても面倒ですので、まず単純に可視光の強さを求め、 その可視光よりも高い周波数の光を紫外線、 可視光よりも低い周波数の光を赤外線という風に、３つに分けただけです。
　紫外線の更に上のエネルギー、Ｘ線やガンマ線も一緒にしてしまいました。 Ｘ線やガンマ線は大気によって割合が大きく、地表に届くことはほとんど有り得ません。 紫外線の中に含めることで、紫外線自体の評価が歪んでしまった可能性もあります。

　さて、どうなるのでしょうか。


　　　　　　　　　　　　　　　　表３　太陽光の成分比率（主系列星の場合）

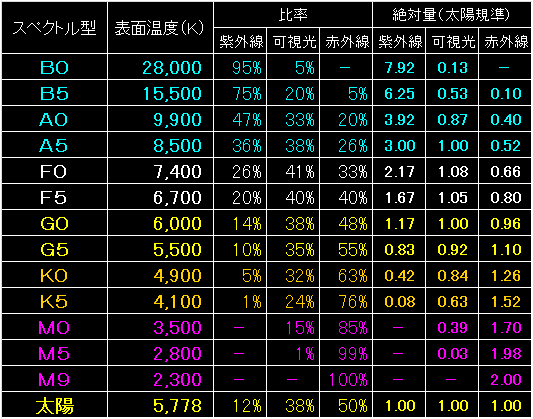
　上の表は、ヴィーンの変位則から、太陽光の成分比率を求めた結果です。
　これによると、ソル（太陽）から放射されるエネルギー（太陽光）の内、 12％が紫外線、38％が可視光、50％が赤外線に大別できました。 これを基準にして、他のスペクトル型についても考察します。



　まず、表面温度の低いスペクトル型ですが、 スペクトルＫ型の太陽光は紫外線をほとんど含みません。
　ソル（太陽）を基準とすれば、 Ｋ０型は0.42（42％）、Ｋ５型になると0.08（8％）しか存在しないのです。
　日焼けに悩む女性には喜ばれそうですが、その代わりビタミンＤの活性化ができないので、骨が脆くなってしまうでしょう。 人工的な紫外線浴（もしくは、それに代わるハイテク手段）が必要不可欠になりました。
　可視光の強さも0.84〜0.63（84〜63％）で弱めです。ちょっと日差しが弱く感じるという程度でしょうか。 とは言っても青色光が少ないので青や紫といった色合いのものは暗くなり、ほとんど黒と見分けが付きません。
　この世界原産の植物は、主に赤色光で光合成を行うことになるでしょう。 赤色光を効率良く吸収するため、植物の葉緑素は緑色ではなく、青色になります。
　赤外線の強さは1.26〜1.52（126〜152％）ですから、あまり明るくないのに暖かい、という風になりそうです。

　スペクトルＭ型に照らされた世界はもっと極端です。
　紫外線の量は１％未満で、ソル（太陽）とは比べようがありません。 この世界の大気には、ほとんどオゾンが含まれていないでしょう。 この世界原産の動植物は、紫外線への耐性もほとんどない筈です。
　可視光も、Ｍ０型で0.39（39％）と薄曇り状態。 Ｍ５型で0.03（3％）の雨天の屋外か照明された屋内レベルです。 Ｍ９型では0.01（1％）未満ですから更に薄暗い雰囲気となっているでしょう。
　その分、残りのすべてのエネルギーが赤外線となっていますので、暖かさだけは十分です。 例えるならば、電気コタツの中、でしょうか。
　真面目に考えると、こうした世界は日中でも薄暗く屋外照明が欠かせません。 また、こうした世界で育つ植物は専ら赤外線を吸収して光合成を行っているのでしょう。 赤外線ゴーグルを通して見れば、植物の葉は真っ黒になります。
　そうした世界の風景を考えるのは、想像力のない私には荷が重いようです。



　反対に、表面温度の高いスペクトル型はどうでしょう。
　スペクトルＦ型の太陽光は、ソル（太陽）に比べると 紫外線の強さが2.17〜1.67倍（217〜167％）です。日焼けが酷いことになりそうですね。 リジャイナ（主恒星のスペクトルはＦ７）の海水浴場に遊びに行っても、ビキニ姿の女性を見ることは難しいでしょう。
　可視光の強さは1.08〜1.05（108〜105％）なので同程度ですが、可視光の分布は均等です。 太陽光であっても白色蛍光灯のような、白っぽい光として感じられるでしょう。
　植物の葉緑素は、より赤味が増します。 原産植物の茂みは緑ではなく、真紅になっている可能性が高いようです。
　赤外線の強さは0.66〜0.80（66〜80％）です。

　スペクトルＡ型は、紫外線の強さが3.92〜3.00でした。 人間は紫外線遮蔽能力の高い防護服を着ていない限り、短時間で全身火傷を負ってしまいます。 冗談ではなく、地下都市で暮らすか、屋外に出るのは夜間に限るといった制限が必要となるでしょう。
　原産の動物であれば問題なしですが。
　可視光の強さは0.87〜1.00ですので、明るさに問題はありません。しかし分布は紫や青色の方に偏ってきました。 太陽光の下、赤やオレンジといった色合いは、若干くすんで見えるかも知れません。
　赤外線の強さは0.40〜0.52です。

　スペクトルＢ型は、紫外線の強さが7.92〜6.25。
　可視光の強さは0.13〜0.53ですから、かなり薄暗くなりました。
　赤外線の強さは0.10以下で、ほとんど存在しません。



　どうにも、私の当初の予想より極端な数値が出てしまいました。
　Ｆ型やＫ型で説明したように、物の色合いが少し変わって見える、 という程度を期待していたのですが、そんな生易しいレベルでは済まなかったのです。

　トラベラー宇宙において、人類は何の問題もなく平然と、 スペクトルＡ型やＭ型の星系に植民を行っています。
　このあたりはハイテク技術で解決されているということなのか、デザイナーの考慮が足りなかったのか、分かりませんが。
　少なくとも、真面目に太陽光の成分比率を考えると、設定が崩壊するということが判明しました。

　ですからトラベラー宇宙においては、スペクトルＡ型やＭ型の恒星も、 ソル（太陽）とほぼ同じ成分比率の太陽光を放出している、と考えるべきなのでしょう。
　可視光の成分が異なっているだけであり、 スペクトル型は単に、その大きさと光量を示しているだけなのです。
　そうでも解釈しないとやっていられません（苦笑）。

　さて、気を取り直して、別の問題を考察してみましょうか。

　最初の方でも少し触れましたが、とある世界（惑星や衛星）が住み易い環境であるためには、 その星系の主恒星から受け取るエネルギー量が、ある一定の範囲に収まっていなければなりません。
　受け取るエネルギー量が多過ぎれば、金星（Venus）のような灼熱地獄になってしまいます。
　反対に少な過ぎれば、火星（Mars）のような酷寒地獄が待っているでしょう。

　困ったことに、主恒星のスペクトル型が変わると、その主恒星から放出されるエネルギー量も増減します。
　当然ながら、そのスペクトル型（エネルギー量）に合わせて、公転軌道を動かさなければなりません。
　エネルギー量が多い主恒星ならば公転軌道を外側に、少ない主恒星ならば公転軌道を内側に動かすことで、 世界が受け取るエネルギー量を調整することになる訳です。

　ちなみに、スペクトルＧ２型の主系列星である太陽（Sol）の場合、 エネルギー量が適切となる距離は1.0AU（天文単位）でした。
　今現在、地球（Terra）が巡っている公転軌道の半径そのものですが、トラベラーにおいて 快適な環境の居住世界が存在できる公転軌道のことを「可住圏」と呼びます。
　幾つかの例外は有り得ますが、トラベラーのルール上、主要世界の多くは「可住圏」に配置されています。 ですから、それぞれの星系の「可住圏」を求めておくことは、今後の考察でとても重要になってきました。



　特定星系の「可住圏」を求める方程式は「CT版偵察局、p.29」に掲載されており、 自分でも計算できますが、面倒なので「MTレフリーズ・マニュアル、p.27」のデータを転載することにしましょう。
　ちなみに、MTレフリーズ・マニュアルの表は、地球と同レベルの反射率（0.3）と温室効果（1.1）を持った世界が、 快適な温度（年間平均気温が288℃）になる公転距離に「最も近い軌道番号」、という条件で決定されています。
　より正確な気温を求めたい、あるいは、半端な軌道番号でも良いから正確な公転距離を求めたいという場合には、 「CT版偵察局」の計算式を用いなければなりません。
　とても面倒ですが、世界設定の幅が広がるので、とても面白い計算式です。



　「Consolidated MEGATRAVELLER Errata」の訂正が見つかりました。

27ページ、Step15、規模�Tbの恒星の軌道分類（訂正）

　「Ｋ５とＭ０」の軌道番号11は、「Ｈ：可住圏」
　「Ｍ５とＭ９」の軌道番号11は、「Ｉ：内圏」です。

　困ったことに、「Ｋ５とＭ９」の「Ｈ：可住圏」が何処にあるのか、エラッタには明記されていません。
　普通に考えれば「Ｈ：可住圏」はひとつ外側、軌道番号12になると思われます。
　念のため確認したところ、CT版偵察局では、 軌道番号12が可住圏である、と記述されておりました。



　エラッタ訂正込みの可住圏軌道番号を、以下に示します。


　　　　　表４　スペクトル型と恒星規模から決定される、可住圏の軌道番号

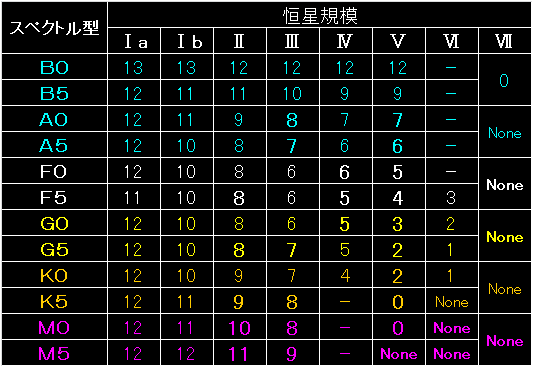
　「None」の表記は、そのスペクトルと恒星規模では、可住圏の軌道を持てないということです。
　恒星規模�XのスペクトルＭ５型（Ｍ５〜Ｍ９）は、 スピンワードマーチ宙域の帝国領内に、なんと56星系（20.6％）もあるのですけれどね。
　ついでに書いておくと、同じように可住圏を持てない 恒星規模�YのスペクトルＭ０〜Ｍ５型（Ｍ０〜Ｍ９）は 10星系（3.7％）、 恒星規模�Z（白色矮星）は７星系（2.6％）も見つかりました。 全部を合わせて73星系（26.8％）です。
　デザイナーは、このあたりの矛盾をどうやって解決するつもりなのでしょう。

　私はCT版偵察局のデータを持っていますから、公転軌道半径0.1AUや0.05AUといった特殊軌道を作り、 そこに主要世界を配置して対応しました。しかしCT版偵察局を持っていない方には無理な対応では？
　このあたり、MT版は不親切だと思います。

　それにしても、恒星規模�Y「準矮星」や恒星規模�Z「白色矮星」を主恒星とした星系でも、 酸素／窒素型の大気（UWPコードの大気レベル２〜９）を持つ世界が存在するという公式設定は厄介な問題です。
　この問題はトラベラーの公式ルールに文句を付けることになってしまうので、あまり真面目に考えたくありませんが。

　白色矮星（規模�Z）の過去を思い浮かべてみれば分かる通り、 現在の可住圏に惑星が存在する筈がないのです。 それでも白色矮星の可住圏に惑星が存在しているとすれば、 それはほぼ間違いなく捕獲惑星でしょう。
　ということは、数千年から数万年…あるいはそれ以上の公転周期を持ち、一瞬だけ主恒星に近づくといった軌道を描いていると思われます。 その一瞬だけでは、とても熱量が足りません。公転周期の大半、惑星は凍り付いてしまいます。

　ひょっとしたら、可住圏にこだわる必要はないかもしれません。 エウロパ等では地熱からのエネルギーで生物が存在できるかもしれないという話を、この状況に当てはめてみましょう。
　捕獲惑星は楕円軌道を描きながら、 その運動エネルギーを地熱に変えるとしたらどうでしょうか？ 　これをエネルギー源として活動する深海生物の存在可能性があります。
　果たしてそうした生物の活動が、その惑星の大気を酸素／窒素型に変えてくれるものかどうか分かりませんが、 その解決はレフリーの想像力にお任せします。プレイヤーが納得できるだけの設定を作り上げて下さい。



　可住圏が存在しない73星系（26.8％）に関する問題は、とりあえず保留しておきますが、 そうした可住圏が存在しない星系であっても 主要世界はできるだけ暖かく（受け取るエネルギー量を多く）しておく方が色々と都合良いでしょう。
　そのため、主恒星にできるだけ近い軌道を巡らせることにしました。 しかしトラベラーの公式ルールにおいて、主恒星に最も近い軌道は、軌道半径0.2AUの軌道番号０しかありません。 必然的に、主要世界は軌道番号０を巡ることになりました。
　今後の考察は、その想定に基づいて進めます。



　主要世界が巡る軌道番号は、主恒星のスペクトル型と恒星規模によって、軌道番号０〜13の範囲に定まりました。
　可住圏が存在しない73星系（26.8％）についても、 それらの星系の主要世界は軌道番号０を巡るということで解決済み。

　今度は、公転周期（主要世界の１年の長さ）を求めてみましょう。


　　　　　　　　表５　可住圏の軌道番号によって決まる、公転周期

　すべてのスペクトル型と恒星規模について、公転周期を計算することは大変です。
　なので、スピンワードマーチ宙域の帝国領内に存在する主恒星のスペクトル型と恒星規模に絞り、 可住圏を巡る主要世界の公転周期を求めました。
　その際は主恒星の質量が必要ですから、表の右端にその数値も載せておきます（質量は太陽を1.0とした倍数表示）。



　計算した公転周期（１年の長さ）は上記の通りなのですが、幾つか説明が必要でしょう。
　例えば軌道番号０を巡る主要世界の公転周期は、主恒星のスペクトル型と恒星規模によって、 最短4.43週間、最長14.47週間という広い範囲の数値になってしまいました。
　これは、スペクトル型と恒星規模、というよりも、主恒星の質量による影響です。
　星系の中心にある質量が大きい（重い）場合、世界を引きつける重力が強くなるため世界はより速く公転しなければならず、 その結果、公転周期が短くなります。
　反対に、星系の中心にある質量が小さい（軽い）場合は、世界を引きつける重力が弱くなるため世界はゆっくりと公転し、 自動的に公転周期が長くなるという訳で。

　そういえば、ルーニオン星域の首都ルーニオンの主恒星は スペクトルＭ３Ｄ型（Ｍ型の白色矮星）だそうです。
　公転周期が４週間と半分（正確には31日）ですから、自然の季節感はほとんどなさそうです。 なんといっても四季の長さが１週間ちょっとしかありませんのでから。

　ちなみに、「もしも太陽の質量がもっと大きかったら？」に掲載されていた 仮想地球の５番目、グランスターの公転周期を計算してみたところ、私の計算では3.5年になりました。
　上記の本には5.3年と書いてありましたが、これは3.5年の誤訳なのかも知れません。

　主要世界の軌道番号（公転軌道半径）が決まりましたから、次の問題です。

　星系（主要世界）に寄港する商船のジャンプ・ポイントは、
　　　　　　　　　　　　　　　果たして、何処にあるのでしょうか？



　この問題については、「MT版帝国百科」に掲載されている、 主恒星のスペクトル型と恒星規模を見た直後から悩んでおりました。

　御存知のように、私はCT版のキャンペーン・シナリオ「黄昏の峰へ」を愛しております。 それこそ、自由貿易商船の旅を20回もソロ・プレイできるほど。
　それだけプレイ経験を重ねてしまうと寄港する世界の雰囲気（設定）についても熟知してしまい、 改めて提示されたMT版帝国百科の設定に、首を傾げたくなるような矛盾点を見つけてしまう訳なのです。

　例えばダイナムの公転周期は1,600年という設定（CT版シナリオ：灼熱面横断！）がありましたけれど、 主恒星のスペクトルがＡ４�Vでしたら、可住圏の軌道番号は７。 公転周期は10年前後になる筈では？　とか。
　ジェンゲやレックの主恒星は揃ってＭ０�Xですから、 可住圏は軌道番号０のみ。
　軌道番号０は世界の規模を決定する際にDM−５が加算されるので、世界の規模は５以下にしかならない筈。 でもジェンゲの規模は７で、レックは９でした。星系作成のルールに矛盾していないのかな？　とか。
　すでに主要世界の設定が存在して、その上で星系作成を行ったという解釈も考えられるのですが、 その際はスペクトル型を決定する際のサイコロにDM＋４が加算されます。 そうすると、主恒星のスペクトルがＭ型になる可能性は、ほとんどありません。



　上記のような設定／ルール上の矛盾解決は後回しにしておきましょう。
　それよりも、ずっと気になる問題がひとつ見つかってしまいました。

　例にも出したジェンゲおよびレック星系、主恒星がＭ０�X型の星系において、 可住圏は軌道番号０となります。 当然、多くの星系において主要世界は可住圏、 軌道番号０（公転半径0.2AU）に存在するでしょう。
　しかし私は、とあるデータから、Ｍ０�X型の100倍直径が0.55AUであることを知っておりました。
　考えるまでもないことですが、0.2AU ＜ 0.55AU、です。
　つまり主要世界が主恒星の100倍直径の内側に存在している訳ですね。

　レック星系を訪れる商船は、直接、主要世界レックの100倍直径にジャンプアウトできません。
　主要世界レックの100倍直径へ近付くより先に、主恒星の100倍直径によって、ジャンプ空間から弾き出されてしまうのです。
　主恒星の100倍直径でジャンプアウトした商船は、主要世界レックまで0.35AU（＝主恒星の100倍直径0.55AU−主要世界の公転半径0.2AU）の距離を、 通常ドライブで移動しなければなりません。
　星系を離脱する（ジャンプインする）際も同様。
　主要世界レックの100倍直径に到達しても、その場所はまだ、主恒星の100倍直径の内側です。
　安全にジャンプするためには、主恒星の100倍直径の外側まで0.35AUの距離を、通常ドライブで移動しておかなければなりません。

　こういった数字が出て来ると、その星系の可住圏が 主恒星の100倍直径の内側にあるか、外側にあるか、気になってきませんか？




（１）主恒星のジャンプ不能圏（100倍直径）

　という訳で、以下に主恒星の100倍直径の大きさを、AU（天文単位＝１億５千万km）で示しました。


　　　　表６　スペクトル型と恒星規模から決定される、100倍直径の大きさ

　大きさの単位がAUなので、ちょっと分かり難いかも知れません。
　しかし軌道番号で表記するともっと分かり難くなるので、こうしました。
　ちなみに公転軌道半径は、軌道番号０が0.2AU、軌道番号１が0.4AU、 軌道番号２が0.7AU、軌道番号３が1.0AU、という風に定義されております。

　この100倍直径の大きさを、可住圏の軌道番号（公転軌道半径）と比較し、100倍直径の方が大きければ「内側」、 公転軌道半径の方が大きければ「外側」だと判断します。



　ひとつずつ数値を比較するのも面倒ですから、すでに比較済みのデータを載せてしまいましょう。
　以下の表を御覧ください。


表７　可住圏が100倍直径の内側に入ってしまう主恒星の、スペクトル型と恒星規模

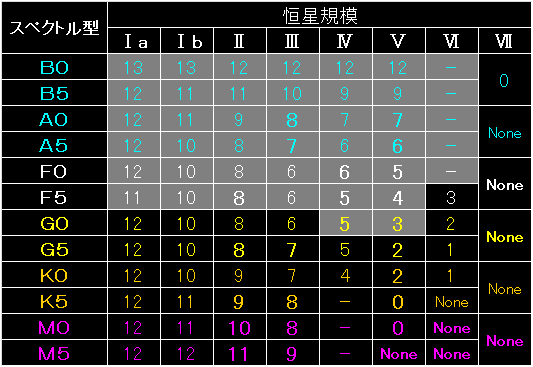
　この表は、前述の表４をコピーして、部分的に変更したものです。
　ですから表に示した数字は、可住圏の軌道番号となりました。

　数字は表４そのままですが、マス内の色が黒のままである部分は、可住圏が主恒星100倍直径の「内側」にあることを、 マス内が灰色に変わった部分は、可住圏が主恒星100倍直径の「外側」にあることを示します。

　結果をまとめると、恒星規模「�Ta〜�V（明るい超巨星〜巨星）」の場合は、 スペクトルＦ５以上が「外側」、 スペクトルＧ０以下が「内側」です。
　恒星規模「�W〜�X（準巨星〜主系列星）」の場合は、 スペクトルＧ０以上が「外側」で、 スペクトルＧ５以下が「内側」でした。
　恒星規模「�Y（準矮星）」は、存在するすべてのスペクトル型が「内側」に存在。
　恒星規模「�Z（白色矮星）」の場合は、そもそも可住圏となる軌道番号が存在しません。 しかし私なりの判断で主要世界は0.01〜0.005AUの公転半径を巡っていると考えました。 ですから、すべてのスペクトル型が「内側」になります。



　すべての恒星規模において、 スペクトルＭ型とスペクトルＫ型、 一部のスペクトルＧ型が、「内側」です。
　何となく、嫌な予感がしてきませんか？
　スピンワードマーチ宙域の帝国領内において、その半分以上の星系がスペクトルＭ型だったと私は記憶しているのです。

　確かめてみましょう。


　　　　　　表８　主要世界が主恒星の100倍直径に収まってしまう星系の数

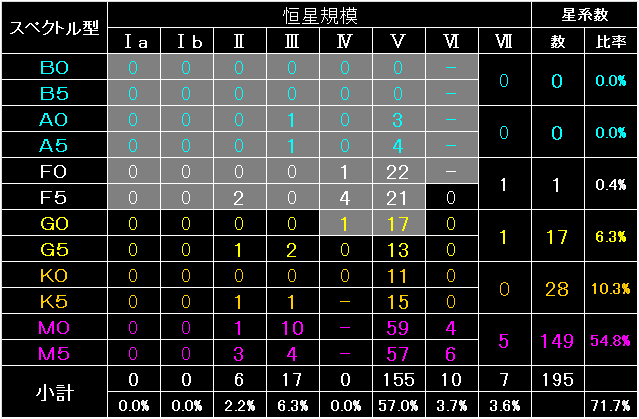
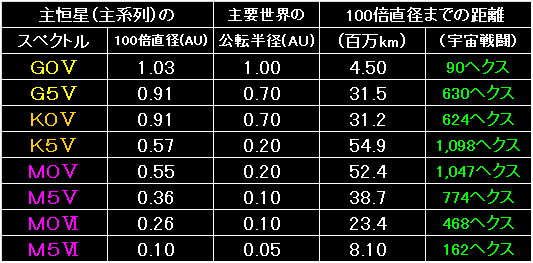
　これは表１のコピーですが、右端の星系数は、可住圏を巡る主要世界が、 主恒星の100倍直径の「内側」に存在する星系数を示しています。

　スピンワードマーチ宙域の帝国領は、272星系。
　その内195星系（71.7％）の主要世界が、主恒星の100倍直径の「内側」であると判明しました。

　それらの星系に寄港する際、主要世界の100倍直径までの距離を移動するだけでは済みません。
　最短でも、主恒星の100倍直径から、主要世界（可住圏）の公転軌道半径を引いた距離、 それだけの移動を行わなければならないでしょう。




（２）ジャンプ・ポイントまでの移動距離と時間（主系列星と準矮星）

　今度は、主要世界からジャンプ・ポイントまでの距離を求めます。

　一般的な商船は、星系内の移動時間を最短にしなければなりません。
　移動時間を最小限に留め、残り時間は商談や休息に使う。
　それが商船のあるべき姿です。 密輸業者や遊覧目的のヨットであれば別の経済原理で動きますから話は別ですが、 一般的な商船にとって「時は金なり」なのです。

　移動時間を小さくするためには、２つの方法があります。
　加速度を大きくするか、あるいは、移動距離を小さくするか。

　商船の加速度を大きくする方法は、節約できる経費よりも増える経費の方が大きいので却下。 最も経済的な加速度は１Ｇ加速なのです。

　経済的理由により加速度が１Ｇで確定しているのであれば、後は移動距離を小さくする以外にありません。
　という訳で、主要世界を出港した商船は主恒星に船尾を向けて、星系のまっすぐ外側へ加速することになるでしょう。
　その針路を取ることによって、ジャンプが可能な100倍直径の外側まで、最短距離を移動することができます。

　その最短距離は、主恒星の100倍直径の大きさから、主要世界の公転軌道半径を引くことで得られます。
　さて、その結果はどうなるでしょう。
　まず、恒星規模「�X〜�Y（主系列星〜準矮星）」について、最短距離をまとめました。 恒星規模「�Z（白色矮星）」については、似たような数値になるので計算していません。


　　　　　　　　表９　主恒星のスペクトル型と、星系内移動距離の関係

　主要世界の公転軌道半径が、主恒星100倍直径の「内側」に存在する星系について、 まず、公転軌道半径と主恒星の100倍直径を比べました。



　スペクトルＧ０�X型（Ｇ０〜Ｇ４）の場合、計算結果が少し複雑です。
　細分化されたスペクトル型によって、主要世界が「内側」になるか、 「外側」になるか、が異なるのです。

　Ｇ０〜Ｇ１の場合、主要世界は少しだけ「内側」に入りました。
　最短の移動距離はＧ０で450万kmですから、通常の惑星の100倍直径よりも遠い距離まで移動しなければなりません。
　しかし主要世界がガス・ジャイアントの衛星だった場合、ガス・ジャイアントの100倍直径は500万〜1,000万kmですので、 主恒星の「内側」に入っていても、特に移動距離は増えないでしょう。
　もちろん、移動方向が主恒星から離れる方向に限られるという制限は付きますが。

　Ｇ２の場合、主要世界は、主恒星の100倍直径の境界線上にあります。
　移動距離は、主要世界の100倍直径と同じ移動距離で済みますし、主恒星に近付こうとしない限り、移動方向も自由です。

　Ｇ３〜Ｇ４の場合、主要世界は「外側」になりました。
　主要世界の100倍直径まで離れれば安全にジャンプできますし、移動方向も完全に自由です。



　スペクトルＧ５�X型、スペクトルＫ０�X型、Ｋ５�X型、 スペクトルＭ０�X型の場合、細分化されたスペクトルのすべてが「内側」です。
　一番、移動距離が長いスペクトルはＫ５�X型になりました。
　ほぼ同距離でＭ０�X型も並んでいますが。



　スペクトルＭ５�X型、Ｍ０�Y型、 Ｍ５�Y型の星系は、公式ルールにおいて可住圏が存在しません。 しかし主要世界が生存可能な世界（呼吸可能な大気を持つ世界）である以上、そうした矛盾は困りませす。 ですから私は、公転軌道半径が0.1AU、0.05AUといった特殊軌道を作り、そこに主要世界を置くことにしました。
　ハウス・ルールであることは自覚していますが、これ以外に矛盾を解決できる方法を思いつかないのです。 何か良い考えがあったら教えて下さい。

　このような理由により、 スペクトルＭ５�X型とＭ０�Y型の主要世界は公転軌道半径0.1AUを、 スペクトルＭ５�Y型の主要世界は公転軌道半径0.05AUを巡っていることにしました。
　その公転軌道半径を用いた計算結果が、表９の数字になっています。



　とりあえず、ジェンゲ星系とレック星系は、主要世界からジャンプ・ポイントまでの距離が５千万km超であると判明しました。
　今度は、その移動距離から移動時間を求めてみましょう。
　商船の移動が前提ですので、加速度を１Ｇで計算しています。


　　　　　　　　表10　主恒星のスペクトル型と、星系内移動時間の関係

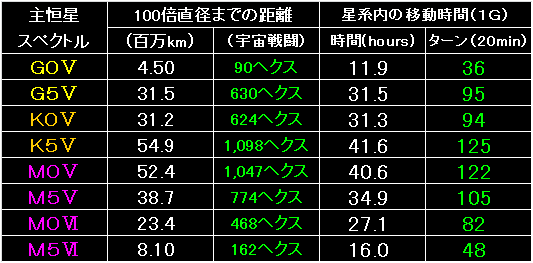
　移動時間は、御覧の通りです。

　スペクトルＧ０�X型（Ｇ０〜Ｇ４）は既に述べた通り、細分化されたスペクトルによって移動距離が変わります。
　Ｇ０の場合は上記のように、移動時間が12時間に増えるでしょう。 大した増え方ではないので「外側」扱いでも構いません。



　スペクトルＧ５�X型〜Ｍ０�X型の場合、星系内移動時間は32〜42時間に増えました。
　例に出した主要世界、ジェンゲの規模は７、レックの規模は９ですから、 これまでは６〜７時間の星系内移動で済んだはずです。
　MT版で、世界データに主恒星のスペクトル型が追加されたため、移動時間が26〜35時間も増えてしまいました。 星系内移動は、星系到着時と離脱時の２回が必要ですから、増えた移動時間も２倍で52〜70時間（２日強〜３日弱）です。
　これだけの時間を星系内移動に費やしてしまうと、何だか、物凄くもったいない気分になりませんか？




（３）ジャンプ・ポイントまでの移動距離と時間（巨星）

　今度は、恒星規模「�U〜�V（明るい巨星〜巨星）」について、 移動の最短距離をまとめました。


　　　　　　　　表11　主恒星のスペクトル型と、星系内移動距離の関係

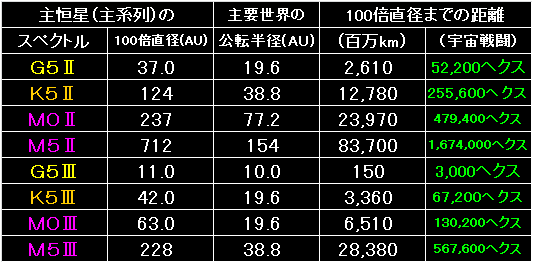
　上の表も、公転軌道半径と主恒星の100倍直径を比べた結果を示しています。

　御覧の通り、星系内を移動しなければならない距離、100倍直径までの距離が、とても大きなものになってしまいました。
　これはもともとスペクトルＫ型、Ｍ型タイプの巨星が 文字通り「膨れ上がっている」ことに起因しているのでしょう。
　ジャンプを安全に行える距離「100倍直径」は、主恒星の直径を100倍したものです。 主恒星の直径が「膨れ上がっている」のであれば、 その100倍直径も比例して「膨れ上がる」のですから。



　例えば、スペクトルＭ５�U型の巨星は、100倍直径の大きさが712Uになりました。
　可住圏が軌道番号11で、その軌道半径は154AUです。
　その差は何と558AU（＝712−154）。ソル星系（太陽系）を端から端まで移動しても、まだ足りないほどの長距離ですね。

　これだけの距離を通常ドライブで横切ると、どれだけの時間が掛かるのでしょうか。移動時間を求めてみましょう。
　今回も商船の移動が前提ですので、加速度は１Ｇです。


　　　　　　　　表12　主恒星のスペクトル型と、星系内移動時間の関係

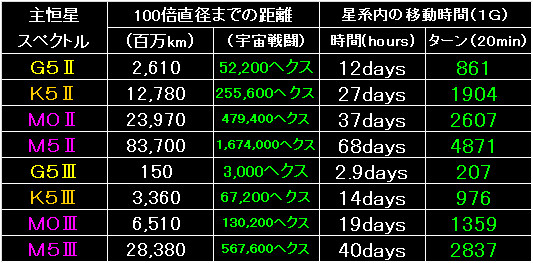
　凄い数字が出てきました。



　スペクトルＧ５�V型の移動時間、2.9日については、まだ許容範囲だと許せます。

　しかしスペクトルＧ５�U型の12日、Ｋ５�V型の14日は、 商船の一般的な星系滞在時間である７日を明らかに超えてしまっています。

　そして最大値を示しているＭ５�U型は68日。
　ジャンプポイントから主要世界まで、星系内移動を２か月も必要とする星系の存在は、あまりにも非常識です。往復を考えれば２倍の４ヶ月ですね。
　トラベラー世界における商船の基本行動パターン、１週間のジャンプと１週間の星系滞在の繰り返しには、どう考えてもふさわしくありません。
　公式設定や世界観に矛盾が生じてしまいます。
　一体、何が間違っているのでしょうか？



　ここで、MAG様の考察「Jump MSD (Jump Drive)」を読み直しましょう。
　今回の考察で私が気付いた問題点はすでに多くの方によって議論されており、その解決策も提案済みでした。

　その要点は、以下のような主張にまとめられます。

　いわゆる100直径といったジャンプ制限が重力の大きさで定まっているとすると， 地球は太陽のジャンプ制限に抵触してしまうといったおかしなことが生じます。
　これでは，恒星の重力圏外まで移動するために，通常ドライブによる長時間の移動を強制されることとなり， 宇宙船運行における，ジャンプ１週間，停泊１週間という基本概念が大きく崩れてしまいます。
　…中略…
　100直径制限は重力ではなく重力偏差に基づき説明するのが適当であろう。
　…中略…
　100直径制限は実は商船のパーサーなどが乗客に対して簡易に説明する目安のようなもので， 熟練した乗員達は別に正確な最小安全距離 MSD (minimum safe distance) を算出しているのだ。

　という訳で、今度は重力偏差に基づく最小安全距離を求めてみることにします。

　MAG様の考察「Jump MSD (Jump Drive)」を参考にして、 重力偏差（重力勾配）に基づいた最小安全距離を計算してみました。




（１）主恒星のジャンプ不能圏（最小安全距離）

　従来の「100倍直径」は単純に、主恒星の直径を100倍しただけです。
　そこには主恒星の質量も密度も全く考慮されておりません。
　もっとも、通常の惑星（鉄／ニッケルを核とした地球型惑星）であれば、 100倍直径≒最小安全距離が成り立ちます。
　ですから主要世界の最小安全距離を求めることが面倒な場合は、100倍直径で代用しても構わないでしょう。


　「最小安全距離」は、まず主恒星の質量が重要なパラメータとなります。
　そして重力偏差の強さは主恒星からの距離の３乗に反比例していました。

　こうした計算式によるジャンプ不能圏は、どんな大きさになるのでしょうか。
　以下に、主恒星の最小安全距離を、同じ単位のAUで示します。


　　　表13　スペクトル型と恒星規模から決定される、最小安全距離の大きさ

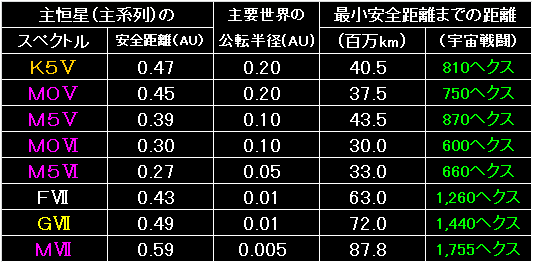
　これは、表６の100倍直径を、最小安全距離に置き換えたものです。
　ついでに可住圏の公転軌道半径と大きさを比較し、 「内側」か「外側」かの判別も済ませました。

　マス内の色が黒のままである部分は、 可住圏が主恒星最小安全距離の「内側」にあることを、 マス内が灰色に変わった部分は、 可住圏が主恒星最小安全距離の「外側」にあることを示します。



　100倍直径を最小安全距離に置き換えた結果は、実に劇的です。
　100倍直径の分布範囲は0.006〜3,020AUという広いものになっていました。
　それに対して恒星の質量は、太陽を基準として0.1〜60の範囲内にありますから、 その質量から求めた最小安全距離は、0.27〜2.22AUの範囲に収束するのです。

　恒星規模「�Ta〜�W（明るい超巨星〜準巨星）」の場合、あらゆるスペクトル型において、 主要世界は最小安全距離の「外側」に存在します。
　このため、スペクトルＭ型の巨星であっても、星系内移動時間が延びることは有り得ません。 表12の恐ろしい結果を知るだけに、とても嬉しい変化でした。
　実は、恒星規模「�Ta〜�U（明るい超巨星〜明るい巨星）」のスペクトルＭ型は、 その低密度故、恒星内部へジャンプアウトできる／しなければならないのではないか、 という不安が生じておりますが、厄介な問題なので気付かなかったことにしましょう。

　恒星規模「�X（主系列星）」の場合は、 スペクトルＫ０以上が「外側」で、 スペクトルＫ５以下が「内側」になりました。
　残念ながら最も数の多いスペクトルＭ型の主系列星は、 最小安全距離を用いても「内側」に存在するのです。

　恒星規模「�Y（準矮星）」の場合は、 スペクトルＧ０以上が「外側」で、 スペクトルＧ５以下が「内側」。

　恒星規模「�Z（白色矮星）」は可住圏が存在しませんが、主要世界が軌道番号０、 公転軌道半径0.2AUの距離を巡っていると想定しても、すべてのスペクトル型が「内側」となりました。
　実際のところ、主要世界は公転半径0.005AU〜0.01AUの軌道を巡っていると考えられますので、 そうした場合も間違いなく「内側」ですが。



　スピンワードマーチ宙域の帝国領内272星系において、 主要世界が最小安全距離の「内側」に存在する星系の数は、以下の通りです。


　　　　表14　主要世界が主恒星の最小安全距離に収まってしまう星系の数

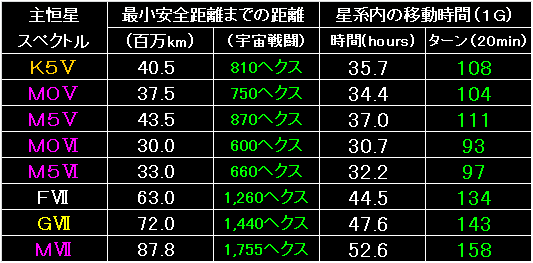
　これは表８をアレンジしたものです。
　右端の星系数は、可住圏を巡る主要世界が、主恒星の最小安全距離内に存在する星系数。

　スピンワードマーチ宙域の帝国領は272星系ですが、その内148星系（54.4％）の主要世界が、 最小安全距離の「内側」であると判明しました。

　最も数の多い主恒星タイプ、恒星規模「�X（主系列星）」のスペクトルＭ型が 最小安全距離の「内側」に存在しますので、劇的に数を減らすことにはなりません。
　全体として数は40星系も減りましたし、恐ろしい移動距離を強要する巨星「（恒星規模�U〜�V）」が 「外側」に変わっただけでも有り難いと思うべきなのでしょうが。




（２）ジャンプ・ポイントまでの移動距離と時間

　主要世界からジャンプ・ポイントまでの距離を求めます。
　主恒星の最小安全距離から、主要世界の公転軌道半径を引いてみましょう。

　その結果を以下に示します。


　　　　　　　　表15　主恒星のスペクトル型と、星系内移動距離の関係

　主恒星最小安全距離の「内側」に主要世界が存在する星系について、 主要世界の公転軌道半径と、主恒星の最小安全距離を比べました。



　スペクトルＫ０�X型とスペクトルＭ０�X型の場合、 可住圏は軌道番号０で、主要世界は公転軌道半径0.2AUの距離に存在します。
　主恒星の最小安全距離は0.47〜0.45AU。
　その差である0.27〜0.25AU（＝4,050万〜3,750万km）が、星系内移動の最短距離になりました。



　スペクトルＭ５�X型とＭ０�Y型、Ｍ５�Y型の場合、 公式ルールでは可住圏が存在しません。しかし可住圏がないと困ってしまうのでハウス・ルールとして、 公転軌道半径が0.1AU、0.05AUといった特殊軌道を作り、そこに主要世界を置いています。
　星系内移動の最短距離も、その公転軌道半径を用いました。
　主恒星の最小安全距離は0.39〜0.27AU。
　その差である0.29〜0.20AU（＝4,350万〜3,000万km）が、星系内移動の最短距離になりました。

　主要世界の公転軌道を公式ルール通りの軌道番号０、公転軌道半径0.2AUとするのであれば、 最短距離は0.19〜0.07AU（2,850万〜1,050万km）になります。



　恒星規模�Z（白色矮星）のスペクトルＦ�Z型、Ｇ�Z型、 Ｍ�Z型の場合も、ルール上は可住圏が存在しません。
　ハウス・ルールで無理やり可住圏を作った場合、その軌道の公転半径は0.01〜0.005AUになります。
　主恒星の最小安全距離は0.43〜0.59AU。
　公転軌道半径を0.01〜0.005AUにした場合、星系内移動の最短距離は0.42〜0.585AU（6,300万〜8,780万km）でした。

　ちなみにロシュの限界は0.004AU前後なので、ぎりぎり大丈夫の筈です。
　とは言うものの、主系列星だった頃、この軌道は主恒星の表面ぎりぎりの筈であり、 こんな近くに惑星が存在できたのか不思議で仕方ありません。
　白色矮星を主恒星とした星系に、呼吸可能な大気付きの主要世界を配置した、 GDWのゲーム・デザイナーがすべて悪いのですが。

　主要世界の公転軌道を公式ルール通りの軌道番号０、公転軌道半径0.2AUとするのであれば、 最短距離は0.22〜0.39AU（3,300万〜5,850万km）です。



　最小安全距離を求めたところ、ジェンゲ星系とレック星系における星系内移動距離は3,750万kmに変わりました。
　大きな変化ではありませんが、およそ３割の低減です。

　再び、移動距離から移動時間を求めてみました。商船の移動ですので、加速度は１Ｇです。


　　　　　　　　表16　主恒星のスペクトル型と、星系内移動時間の関係

　今回も移動時間は、御覧の通り。



　恒星規模「�X〜�Y（主系列星〜準矮星）」を主恒星にした星系において、 星系内移動の時間は30.7〜37.0時間になりました。星系到着時と離脱時の２回で61.4〜74.0時間（２日半〜３日強）です。
　例に出した主要世界、ジェンゲとレックの場合は34.4時間、往復で68.8時間（３日弱）でした。
　これらのタイプの主恒星については、100倍直径も最小安全距離も、それほど移動時間が変わりません。



　恒星規模「�Z（白色矮星）」の場合、星系内移動の時間は44.5〜52.6時間です。 ２倍にすると89.0〜105.2時間（４日弱〜４日強）でした。
　主要世界に３日しか滞在できないというのは、ちょっと不都合があるように思えます。 この矛盾点は、星系内航行中に旅客や貨物／投機貿易品の手配を無線通信で済ませているとか、 それらの手配を３日以内に完了できるほど宇宙港のサービスが迅速あるとか、何か納得できる理由が必要でしょうね。

　主要世界が軌道番号０を巡っているとしても、 最小安全距離との往復時間は66.0〜86.0時間（３日弱〜３日半）で、あまり変わりません。
　主要世界が軌道番号１ならば公転軌道半径は0.4AUですから、 往復時間は41.2〜60.0時間（２日弱〜２日半）になります。かろうじて許容範囲だと言えるでしょう。
　白色矮星から0.4AUも離れると、その主要世界は凍り付いてしまいますが（平均気温は−240℃）。

　どうにも難しい問題です。
　何か落としどころを見つけなければなりませんが、果たして見つかるのでしょうか？

　今回は、主恒星（Primary Star）のスペクトル型と恒星規模について考察しました。



　まずはスピンワードマーチ宙域の帝国領272星系について、主恒星のスペクトル型と恒星規模を集計しています。

　主恒星の多くは恒星規模「�X（主系列星）」でした。
　その数は222星系で、比率は81.6％です。

　スペクトル型に関してはＭ型が最も多く、149星系の54.8％。
　次点がＦ型。星系数51で18.8%。
　３番目がＧ型。星系数35で12.9％。
　４番目がＫ型。星系数28で10.3％。
　５番目がＡ型。星系数９で3.3％。
　帝国領内にＢ型は存在しませんでした。

　ソル（太陽）とは異なるスペクトル型の主恒星からどのような成分の太陽光が放出されているのか。
　恒星の表面温度とヴィーンの変位則から求めてみました。
　しかし残念なことですが、真面目に太陽光の成分比率を考えると設定が崩壊すると判明。これ以上の考察を諦めております。



　次の考察は「可住圏」の軌道番号決定と、その公転周期の算出。
　主要世界の巡る軌道番号と主恒星の質量にもよりますが、 その範囲は最短４週間〜最長1,205年の範囲になりました。



　最後は、主恒星の100倍直径について考察しています。
　スピンワードマーチ宙域の帝国領内272星系について調べたところ、195星系（71.7％）が 主恒星の100倍直径の内側に存在すると判明しました。
　それらの星系において主要世界に寄港する商船は、主要世界の100倍直径よりも遠い場所、 主恒星の100倍直径でジャンプを行わなければなりません。
　特に恒星規模「�U〜�V（明るい巨星〜巨星）」においては、その移動距離と時間が大きな問題となります。 移動時間は最長で68日（＝２ヶ月超）を必要とするため、商船の本行動パターン、１週間のジャンプと１週間の星系滞在の繰り返しには、 どう考えてもふさわしくありません。
　公式設定や世界観に矛盾が生じてしまいます。

　そこで今度は、MAG様の考察「Jump MSD (Jump Drive)」を参考にして、 重力偏差（重力勾配）に基づいた最小安全距離を計算してみました。
　その結果、主恒星の最小安全距離の内側に存在する主要世界は、 148星系（54.4％）まで減少。
　恒星規模「�U〜�V（明るい巨星〜巨星）」の最小安全距離が小さくなったため、 星系内移動に68日（＝２ヶ月超）を必要とする状況は、見事に解決されました。
　実は同時に、恒星規模「�Ta〜�U（明るい超巨星〜明るい巨星）」のスペクトルＭ型は、 その低密度故、恒星内部へジャンプアウトできる／しなければならないのではないか、という不安が生じておりますが。












　2012.05.06　初投稿